Kalibrierung von Funkpolarisationsdaten: Verbesserung der Korrelation zwischen CHIME- und Dwingeloo-Erhebungen

Inhaltsverzeichnis

Abstrakt und 1 Einleitung

1. Faraday-Rotation und Faraday-Synthese

2. Daten & Instrumente

   3.1. CHIME- und GMIMS-Durchmusterungen und 3.2. CHIME/GMIMS Low Band North

   3.3. DRAO Synthesis Telescope Beobachtungen

   3.4. Zusätzliche Datenquellen

3. Merkmale der Kaulquappe

   4.1. Morphologie in Einzelfrequenzbildern

   4.2. Faraday-Tiefen

   4.3. Faraday-Komplexität

   4.4. QU-Anpassung

   4.5. Artefakte

4. Der Ursprung der Kaulquappe

   5.1. Neutrale Wasserstoffstruktur

   5.2. Ionisierte Wasserstoffstruktur

   5.3. Eigenbewegungen von Kandidatensternen

   5.4. Faraday-Tiefe und Elektronensäule

5. Zusammenfassung und Zukunftsaussichten

\ ANHANG

A. AUFGELÖSTE UND NICHT AUFGELÖSTE FARADAY-KOMPONENTEN IN DER FARADAY-SYNTHESE

B. QU-ANPASSUNGSERGEBNISSE

\ REFERENZEN

3.1. CHIME- und GMIMS-Durchmusterungen

3.2. CHIME/GMIMS Low Band North

\

\ Die von uns verwendeten Ringkarten haben keine Strahlentfaltung angewendet. Es gibt kleine Artefakte im Bild, die daraus resultieren, die wir in Abschnitt 4.5 beschreiben, jedoch ist ihre Präsenz nicht hinderlich für die Untersuchung von Strukturen in der Größenordnung von mehreren Grad, wie die Kaulquappe. In dieser Analyse verwenden wir den 400 − 729 MHz Teilbereich des vollständigen CHIME-Bandes, da die höchsten Frequenzen durch Aliasing kontaminiert sind, was die Karten in der interessierenden Region unzuverlässig macht.

\ 3.2.1. Polarisationswinkelkalibrierung

\

\

\

\ Stokes U und V werden aus den Kreuzkorrelationsprodukten gemessen. Wir nehmen an, dass ⟨V ⟩ = 0 vom Himmel in diffuser Emission, da Synchrotronstrahlung in astrophysikalischen Umgebungen mit niedriger Dichte keine zirkulare Polarisation erzeugt. Übersprechen zwischen V und U entsteht durch Phasenverschiebungen. Wir messen eine mittlere Phasenverschiebung ⟨ψ⟩(δ, ν) bei jeder Deklination und Frequenz unter der Annahme, dass ⟨V ⟩ = 0 und berechnen

\

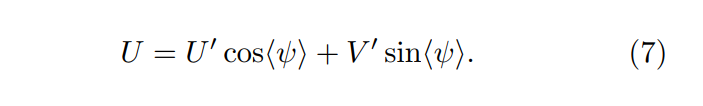
\ Die Annahme ⟨V ⟩ = 0 führt zu qualitativ hochwertigen Anpassungen selbst bei Fast Radio Burst (FRB) Beobachtungen, wo die Annahme eine weniger klare physikalische Rechtfertigung hat als in der diffusen polarisierten Emission, die wir untersuchen (Mckinven et al. 2023). Wir stellen fest, dass die Phasenverschiebung linear in der Frequenz ist, konsistent mit einer Kabelverzögerung τ = ⟨ψ⟩/2πν ∼ 1 ns für die diffuse Emission, wie Mckinven et al. (2021, ihr Anhang A) in CHIME/FRB-Daten gefunden haben.

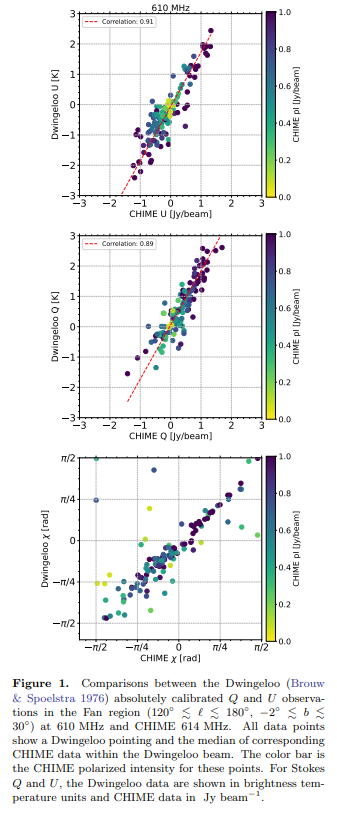
\ In Abbildung 1 vergleichen wir die kalibrierten Daten mit der Dwingeloo-Teleskopuntersuchung bei 610 MHz in der Fan-Region (Brouw & Spoelstra 1976). Es gibt eine starke Korrelation zwischen Dwingeloo U und CHIME U sowie Dwingeloo Q und CHIME Q in jenen Richtungen, für die Dwingeloo-Daten vorliegen, mit Korrelationskoeffizienten R-Werten von 0,91 für U − U und 0,89 für Q − Q Vergleiche. Dies ist eine signifikante Verbesserung gegenüber den unkalibrierten Korrelationskoeffizienten von 0,76 bzw. 0,59. Wir finden ein verbleibendes Übersprechen von bis zu 20% in Stokes Q basierend auf nicht aufgelösten Punktquellenmessungen. Unter Verwendung des mittleren orthogonalen Abstands zwischen jedem Punkt und der angepassten Linie stellen wir fest, dass Rauschen von CHIME- und Dwingeloo-Daten etwa 70% der Streuung in Abbildung 1 beschreibt. Die Polarisationswinkelkorrelation, ebenfalls in Abbildung 1 gezeigt, wird auch durch Kalibrierung verbessert, und die meisten Ausreißer sind Punkte mit niedriger polarisierter Intensität (gelbe Punkte), wo die Unsicherheit im abgeleiteten χ hoch ist.

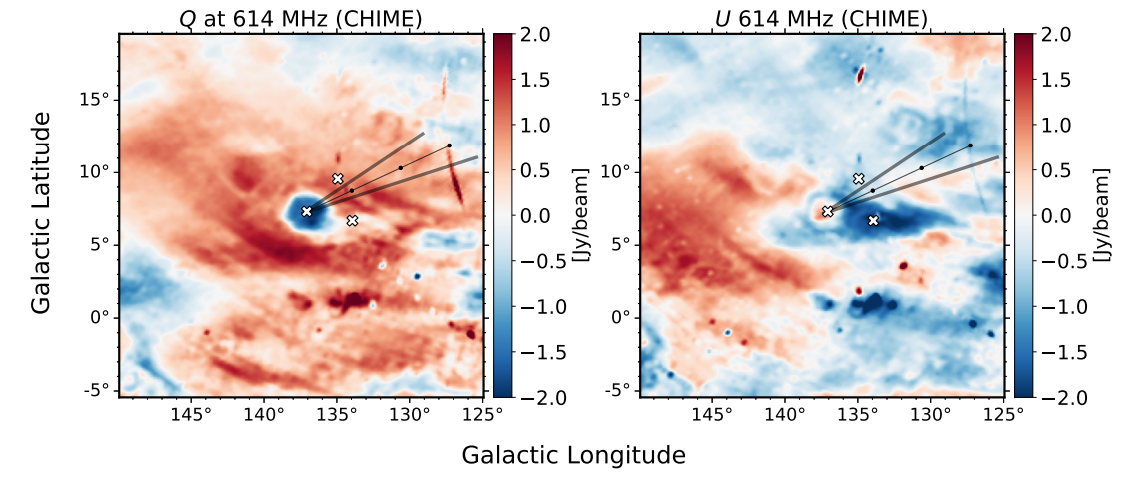
\ Wir zeigen die resultierenden CHIME Q- und U-Karten, mit der χ = 0 Referenzachse zum galaktischen Nordpol gedreht, in Abbildung 2. Während Stokes I zu Q Übersprechen in unseren Daten existiert, kann die Kaulquappenstruktur nicht einfach das Ergebnis von Übersprechen sein. Obwohl es Gesamtintensitätsemission über die gesamte Fan-Region gibt, einschließlich der Kaulquappe, ist diese Emission auf kleinen Skalen strukturlos und kann daher keine falsche Polarisation erzeugen, die der Morphologie der Kaulquappe entspricht. Darüber hinaus kann die Kaulquappe nicht das Produkt von Stokes I-Emission sein, die aus großen Winkelabständen (wie der galaktischen Ebene) stammt und in fernen Nebenkeulen zu sehen ist. Während die fernen Nebenkeulen schlechte Polarisationseigenschaften haben, mittelt sich ihre Polarisation über beträchtliche Bereiche zu niedrigen Werten. Außerdem ist bei linearen Feeds das Übersprechen von I hauptsächlich in Q, nicht in U (in den nativen äquatorialen Koordinaten von CHIME), aber die Kaulquappe ist bereits in Stokes U in äquatorialen Koordinaten erkennbar (nicht gezeigt).

\

\

\ 3.2.2. Faraday-Synthese auf CHIME-Daten

\

\

\ Mit dem rmtools_peakfitcube-Algorithmus in RM-Tools erhalten wir die Spitzen-Faraday-Tiefe und ihren

\

\ zugehörigen Fehler für jedes Spektrum entlang aller Sichtlinien. Die resultierende Karte ist in Abbildung 3b dargestellt. Wir verwenden Spitzen-Faraday-Tiefen anstelle eines ersten Moments (Dickey et al. 2019), um uns auf die Faraday-Tiefe des hellsten Merkmals in jeder Sichtlinie zu konzentrieren, anstatt auf eine gewichtete mittlere Faraday-Tiefe in Faraday-komplexen Regionen.

\ Wir zeigen die integrierte polarisierte Intensität über die Faraday-Tiefenspektren als Nullmomentenkarte in Abbildung 3a. Eine Polarisationswinkelkarte, die durch die Spitzen-Faraday-Tiefe an jedem Pixel zu χ0 zurückgedreht wurde, ist in Abbildung 3c dargestellt.

\

:::info Autoren:

(1) Nasser Mohammed, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Kanada und Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Kanada;

(2) Anna Ordog, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Kanada und Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Kanada;

(3) Rebecca A. Booth, Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Kanada;

(4) Andrea Bracco, INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florenz, Italien und Laboratoire de Physique de l'Ecole Normale Superieure, ENS, Université PSL, CNRS, Sorbonne Universite, Universite de Paris, F-75005 Paris, Frankreich;

(5) Jo-Anne C. Brown, Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Kanada;

(6) Ettore Carretti, INAF-Istituto di Radioastronomia, Via Gobetti 101, 40129 Bologna, Italien;

(7) John M. Dickey, School of Natural Sciences, University of Tasmania, Hobart, Tas 7000 Australien;

(8) Simon Foreman, Department of Physics, Arizona State University, Tempe, AZ 85287, USA;

(9) Mark Halpern, Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1 Kanada;

(10) Marijke Haverkorn, Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, Niederlande;

(11) Alex S. Hill, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Kanada und Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Kanada;

(12) Gary Hinshaw, Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V