Wie WormHole die Pfadfindung in Graphen mit Milliarden von Kanten beschleunigt

Tabelle der Links

Abstrakt und 1. Einleitung

1.1 Unser Beitrag

1.2 Einstellung

1.3 Der Algorithmus

1. Verwandte Arbeiten

2. Algorithmus

   3.1 Die strukturelle Zerlegungsphase

   3.2 Die Routing-Phase

   3.3 Varianten von WormHole

3. Theoretische Analyse

   4.1 Grundlagen

   4.2 Sublinearität des inneren Rings

   4.3 Approximationsfehler

   4.4 Abfragekomplexität

4. Experimentelle Ergebnisse

   5.1 WormHole𝐸, WormHole𝐻 und BiBFS

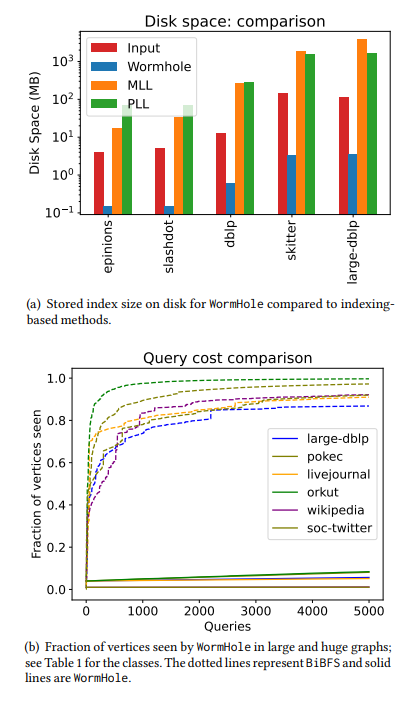
   5.2 Vergleich mit indexbasierten Methoden

   5.3 WormHole als Grundlage: WormHole𝑀

Referenzen

1.1 Unser Beitrag

Wir entwickeln einen neuen Algorithmus, WormHole, der eine Datenstruktur erstellt, die es uns ermöglicht, mehrere kürzeste Pfadanfragen zu beantworten, indem wir die typische Struktur vieler sozialer und Informationsnetzwerke nutzen. WormHole ist einfach, leicht zu implementieren und theoretisch fundiert. Wir bieten mehrere Varianten davon an, die jeweils für unterschiedliche Szenarien geeignet sind und hervorragende empirische Ergebnisse auf verschiedenen Netzwerkdatensätzen zeigen. Im Folgenden sind einige seiner Hauptmerkmale aufgeführt:

\ • Leistungs-Genauigkeits-Kompromiss. Nach unserem besten Wissen ist unserer der erste approximative sublineare Algorithmus für kürzeste Pfade in großen Netzwerken. Die Tatsache, dass wir kleine additive Fehler zulassen, führt zu einem Kompromiss zwischen Vorverarbeitungszeit/-speicher und Zeit pro Anfrage und ermöglicht es uns, eine

\

\ Lösung mit effizienter Vorverarbeitung und schneller Anfrageverarbeitungszeit zu entwickeln. Bemerkenswert ist, dass unsere genaueste (aber langsamste) Variante, WormHole𝐸, eine nahezu perfekte Genauigkeit aufweist: mehr als 90% der Anfragen werden ohne additiven Fehler beantwortet, und in allen Netzwerken werden mehr als 99% der Anfragen mit einem additiven Fehler von höchstens 2 beantwortet. Weitere Details finden Sie in Tabelle 3.

\ • Extrem schnelle Einrichtungszeit. Unsere längste Indexkonstruktionszeit betrug nur zwei Minuten, selbst für Graphen mit Milliarden von Kanten. Zum Vergleich: PLL und MLL haben bei der Hälfte der von uns getesteten Netzwerke eine Zeitüberschreitung erreicht, und für Graphen mittlerer Größe, bei denen PLL und MLL ihre Läufe beendet haben, war die WormHole-Indexkonstruktion 100-mal schneller. Das heißt, WormHole war in Sekunden fertig, während PLL Stunden brauchte. Siehe Tabelle 4 und Tabelle 5. Diese schnelle Einrichtungszeit wird durch die Verwendung eines sublinear großen Index erreicht. Für die größten von uns betrachteten Netzwerke reicht es aus, einen Index von etwa 1% der Knoten zu nehmen, um einen kleinen mittleren additiven Fehler zu erhalten – siehe Tabelle 1. Bei kleineren Netzwerken kann es bis zu 6% sein.

\ • Schnelle Anfrageverarbeitungszeit. Im Vergleich zu BiBFS ist die Vanilla-Version WormHole𝐸 (ohne indexbasierte Optimierungen) für fast alle Graphen 2-mal schneller und für die drei größten von uns getesteten Graphen mehr als 4-mal schneller. Eine einfache Variante, WormHole𝐻, erreicht eine Verbesserung um eine Größenordnung auf Kosten der Genauigkeit: durchweg 20-mal schneller bei fast allen Graphen und mehr als 180-mal schneller für den größten Graphen, den wir haben. Siehe Tabelle 3 für einen vollständigen Vergleich. Indexbasierte Methoden beantworten Anfragen typischerweise in Mikrosekunden; beide der oben genannten Varianten befinden sich noch im Millisekundenbereich.

\ • Kombination von WormHole und dem Stand der Technik. WormHole funktioniert, indem eine kleine Teilmenge von Knoten gespeichert wird, auf denen wir die exakten kürzesten Pfade berechnen. Für beliebige Anfragen leiten wir unseren Pfad durch diese Teilmenge, die wir den Kern nennen. Wir nutzen diese Erkenntnis, um eine dritte Variante, WormHole𝑀, bereitzustellen, indem wir den Stand der Technik für kürzeste Pfade, MLL, auf den Kern implementieren. Dies erreicht Anfrageverarbeitungszeiten, die mit MLL vergleichbar sind (mit der gleichen Genauigkeitsgarantie wie WormHole𝐻), bei einem Bruchteil der Einrichtungskosten und läuft für massive Graphen, bei denen MLL nicht terminiert. Wir untersuchen diesen kombinierten Ansatz in §5.3 und stellen Statistiken in Tabelle 6 bereit.

\ • Sublineare Abfragekomplexität. Die Abfragekomplexität bezieht sich auf die Anzahl der vom Algorithmus abgefragten Knoten. In einem Modell mit eingeschränktem Abfragezugriff, bei dem das Abfragen eines Knotens seine Liste von Nachbarn offenbart (siehe §1.2), skaliert die Abfragekomplexität unseres Algorithmus sehr gut mit der Anzahl der durchgeführten Distanz-/kürzeste-Pfad-Anfragen. Um 5000 approximative kürzeste-Pfad-Anfragen zu beantworten, beobachtet unser Algorithmus nur zwischen 1% und 20% der Knoten für die meisten Netzwerke. Im Vergleich dazu sieht BiBFS mehr als 90% des Graphen, um einige hundert kürzeste-Pfad-Anfragen zu beantworten. Siehe Abbildung 2 und Abbildung 5 für einen Vergleich.

\ • Nachweisbare Garantien für Fehler und Leistung. In §4 beweisen wir eine Reihe theoretischer Ergebnisse, die die empirische Leistung ergänzen und erklären. Die Ergebnisse, die unten informell angegeben sind, werden für das Chung-Lu-Modell von Zufallsgraphen mit einer Potenzgesetz-Gradverteilung [15–17] bewiesen.

\ Theorem 1.1 (Informell). In einem Chung-Lu-Zufallsgraphen 𝐺 mit Potenzgesetz-Exponent 𝛽 ∈ (2,3) auf 𝑛 Knoten hat WormHole mit hoher Wahrscheinlichkeit die folgenden Garantien:

\

\

:::info Autoren:

(1) Talya Eden, Bar-Ilan University ([email protected]);

(2) Omri Ben-Eliezer, MIT ([email protected]);

(3) C. Seshadhri, UC Santa Cruz ([email protected]).

:::

:::info Dieses Paper ist auf arxiv verfügbar unter der CC BY 4.0 Lizenz.

:::

\