Verständnis von Approximationsfehlern und Abfragekomplexität beim WormHole-Routing

Inhaltsverzeichnis

Abstrakt und 1. Einführung

1.1 Unser Beitrag

1.2 Einstellung

1.3 Der Algorithmus

1. Verwandte Arbeiten

2. Algorithmus

   3.1 Die strukturelle Zerlegungsphase

   3.2 Die Routing-Phase

   3.3 Varianten von WormHole

3. Theoretische Analyse

   4.1 Grundlagen

   4.2 Sublinearität des inneren Rings

   4.3 Approximationsfehler

   4.4 Abfragekomplexität

4. Experimentelle Ergebnisse

   5.1 WormHole𝐸, WormHole𝐻 und BiBFS

   5.2 Vergleich mit indexbasierten Methoden

   5.3 WormHole als Grundlage: WormHole𝑀

Referenzen

4.3 Approximationsfehler

Nachdem wir einen sublinearen inneren Ring haben, der den Chung-Lu-Kern enthält, müssen wir zeigen, dass das Routing von Pfaden durch ihn nur eine geringe Strafe verursacht. Intuitiv gilt: Je größer der innere Ring ist, desto einfacher ist dies zu erfüllen: Wenn der innere Ring der gesamte Graph ist, gilt die Aussage trivialerweise. Daher liegt die Herausforderung darin zu zeigen, dass wir auch mit einem sublinearen inneren Ring eine starke Garantie in Bezug auf die Genauigkeit erreichen können. Wir beweisen, dass WormHole für alle Paare einen additiven Fehler von höchstens 𝑂(loglog𝑛) verursacht, was viel kleiner ist als der Durchmesser Θ(log𝑛).

\

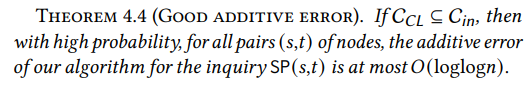
\ Das obige Ergebnis gilt mit hoher Wahrscheinlichkeit selbst im schlimmsten Fall. Das heißt, für alle Paare (𝑠,𝑡) von Knoten im Graphen ist die Länge des von WormHole zurückgegebenen Pfades höchstens 𝑂(loglog𝑛) höher als die tatsächliche Entfernung zwischen 𝑠 und 𝑡. Dies impliziert trivialerweise, dass der durchschnittliche additive Fehler von WormHole mit hoher Wahrscheinlichkeit durch denselben Betrag begrenzt ist.

\

\

4.4 Abfragekomplexität

Erinnern wir uns an das Knotenabfragemodell in diesem Papier (siehe §1.2): Ausgehend von einem einzelnen Knoten dürfen wir iterativ Abfragen durchführen, wobei jede Abfrage die Nachbarliste eines Knotens 𝑣 unserer Wahl abruft. Wir interessieren uns für die Abfragekomplexität, d.h. die Anzahl der Abfragen, die zur Durchführung bestimmter Operationen erforderlich sind.

\ \

\ \ Das erste Ergebnis ist die Obergrenze für unsere Leistung.

\ \

\ \ Beweisskizze. Für eine gegebene Anfrage SP(𝑢, 𝑣) geben wir eine Obergrenze für die Abfragekomplexität der BFS an, die bei 𝑢 beginnt, und ähnlich für 𝑣; die Gesamtabfragekomplexität ist die Summe dieser beiden Größen.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info Autoren:

(1) Talya Eden, Bar-Ilan University ([email protected]);

(2) Omri Ben-Eliezer, MIT ([email protected]);

(3) C. Seshadhri, UC Santa Cruz ([email protected]).

:::

:::info Dieses Papier ist auf arxiv verfügbar unter der CC BY 4.0 Lizenz.

:::

\