Comprendiendo el Error de Aproximación y la Complejidad de Consulta en el Enrutamiento WormHole
Tabla de Enlaces
Abstracto y 1. Introducción
1.1 Nuestra Contribución
1.2 Configuración
1.3 El algoritmo
-
Trabajo Relacionado
-
Algoritmo
3.1 La Fase de Descomposición Estructural
3.2 La Fase de Enrutamiento
3.3 Variantes de WormHole
-
Análisis Teórico
4.1 Preliminares
4.2 Sublinealidad del Anillo Interior
4.3 Error de Aproximación
4.4 Complejidad de Consulta
-
Resultados Experimentales
5.1 WormHole𝐸, WormHole𝐻 y BiBFS
5.2 Comparación con métodos basados en índices
5.3 WormHole como primitiva: WormHole𝑀
Referencias
4.3 Error de Aproximación
Ahora que tenemos un anillo interior sublineal que contiene el núcleo de Chung-Lu, debemos demostrar que enrutar caminos a través de él incurre solo en una pequeña penalización. Intuitivamente, cuanto más grande sea el anillo interior, más fácil es satisfacer esto: si el anillo interior es todo el grafo, la afirmación se cumple trivialmente. Por lo tanto, el desafío radica en demostrar que podemos lograr una fuerte garantía en términos de precisión incluso con un anillo interior sublineal. Demostramos que WormHole incurre en un error aditivo de como máximo 𝑂(loglog𝑛) para todos los pares, que es mucho menor que el diámetro Θ(log𝑛).
\ 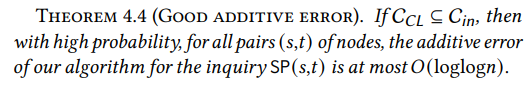
\ El resultado anterior se mantiene con alta probabilidad incluso en el peor de los casos. Es decir, para todos los pares (𝑠,𝑡) de vértices en el grafo, la longitud del camino devuelto por WormHole es como máximo 𝑂(loglog𝑛) mayor que la distancia real entre 𝑠 y 𝑡. Esto implica trivialmente que el error aditivo promedio de WormHole está, con alta probabilidad, limitado por la misma cantidad.
\ 
\
4.4 Complejidad de Consulta
Recordemos el modelo de consulta de nodos en este artículo (ver §1.2): comenzando desde un solo nodo, se nos permite hacer consultas iterativamente, donde cada consulta recupera la lista de vecinos de un nodo 𝑣 de nuestra elección. Estamos interesados en la complejidad de consulta, es decir, el número de consultas necesarias para realizar ciertas operaciones.
\ \ 
\ \ El primer resultado es el límite superior de nuestro rendimiento.
\ \ 
\ \ Esquema de la Prueba. Para una consulta dada SP(𝑢, 𝑣), damos un límite superior en la complejidad de consulta del BFS que comienza en 𝑢, y de manera similar para 𝑣; la complejidad total de consulta es la suma de estas dos cantidades.
\ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \
:::info Autores:
(1) Talya Eden, Universidad Bar-Ilan ([email protected]);
(2) Omri Ben-Eliezer, MIT ([email protected]);
(3) C. Seshadhri, UC Santa Cruz ([email protected]).
:::
:::info Este artículo está disponible en arxiv bajo licencia CC BY 4.0.
:::
\
También te puede interesar

Jubilaciones de Anses: quiénes cobran este jueves 11 de diciembre

El mercado y el invitado
