Le Guide du Geek pour l'Expérimentation en ML

Table des liens

Abstrait et 1. Introduction

1.1 Explication Post Hoc

1.2 Le problème de désaccord

1.3 Encourager le consensus d'explication

1. Travaux connexes

2. Pear : Régularisateur d'accord d'explicateur Post HOC

3. L'efficacité de la formation au consensus

   4.1 Métriques d'accord

   4.2 Amélioration des métriques de consensus

   [4.3 Cohérence à quel prix ?]()

   4.4 Les explications sont-elles toujours précieuses ?

   4.5 Consensus et linéarité

   4.6 Deux termes de perte

4. Discussion

   5.1 Travaux futurs

   5.2 Conclusion, remerciements et références

Annexe

A ANNEXE

A.1 Jeux de données

Dans nos expériences, nous utilisons des jeux de données tabulaires provenant à l'origine d'OpenML et compilés en un ensemble de jeux de données de référence par l'équipe Inria-Soda sur HuggingFace [11]. Nous fournissons quelques détails sur chaque jeu de données :

\ Bank Marketing Il s'agit d'un jeu de données de classification binaire avec six caractéristiques d'entrée et est approximativement équilibré en termes de classes. Nous entraînons sur 7 933 échantillons d'entraînement et testons sur les 2 645 échantillons restants.

\ California Housing Il s'agit d'un jeu de données de classification binaire avec sept caractéristiques d'entrée et est approximativement équilibré en termes de classes. Nous entraînons sur 15 475 échantillons d'entraînement et testons sur les 5 159 échantillons restants.

\ Electricity Il s'agit d'un jeu de données de classification binaire avec sept caractéristiques d'entrée et est approximativement équilibré en termes de classes. Nous entraînons sur 28 855 échantillons d'entraînement et testons sur les 9 619 échantillons restants.

A.2 Hyperparamètres

Beaucoup de nos hyperparamètres sont constants dans toutes nos expériences. Par exemple, tous les MLP sont entraînés avec une taille de lot de 64 et un taux d'apprentissage initial de 0,0005. De plus, tous les MLP que nous étudions comportent 3 couches cachées de 100 neurones chacune. Nous utilisons toujours l'optimiseur AdamW [19]. Le nombre d'époques varie selon les cas. Pour les trois jeux de données, nous entraînons pendant 30 époques lorsque 𝜆 ∈ {0,0, 0,25} et 50 époques dans les autres cas. Lors de l'entraînement des modèles linéaires, nous utilisons 10 époques et un taux d'apprentissage initial de 0,1.

A.3 Métriques de désaccord

Nous définissons ici chacune des six métriques d'accord utilisées dans notre travail.

\ Les quatre premières métriques dépendent des k caractéristiques les plus importantes dans chaque explication. Soit 𝑡𝑜𝑝_𝑓 𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘) représentant les k caractéristiques les plus importantes dans une explication 𝐸, soit 𝑟𝑎𝑛𝑘 (𝐸, 𝑠) le rang d'importance de la caractéristique 𝑠 dans l'explication 𝐸, et soit 𝑠𝑖𝑔𝑛(𝐸, 𝑠) le signe (positif, négatif ou zéro) du score d'importance de la caractéristique 𝑠 dans l'explication 𝐸.

\

\ Les deux métriques d'accord suivantes dépendent de toutes les caractéristiques au sein de chaque explication, pas seulement des k premières. Soit 𝑅 une fonction qui calcule le classement des caractéristiques dans une explication par importance.

\

\ (Remarque : Krishna et al. [15] précisent dans leur article que 𝐹 doit être un ensemble de caractéristiques spécifié par un utilisateur final, mais dans nos expériences, nous utilisons toutes les caractéristiques avec cette métrique).

A.4 Résultats de l'expérience sur les caractéristiques inutiles

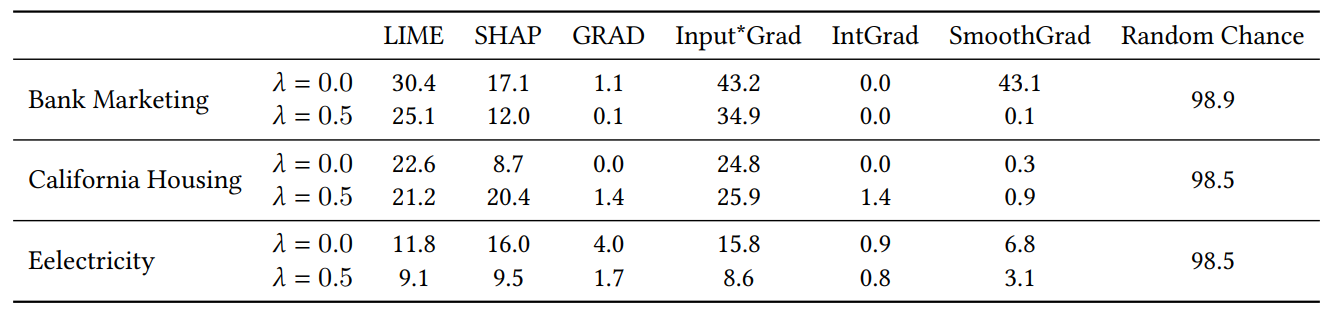
Lorsque nous ajoutons des caractéristiques aléatoires pour l'expérience de la section 4.4, nous doublons le nombre de caractéristiques. Nous faisons cela pour vérifier si notre perte de consensus nuit à la qualité de l'explication en plaçant des caractéristiques non pertinentes dans le top-K plus souvent que les modèles entraînés naturellement. Dans le tableau 1, nous rapportons le pourcentage de fois où chaque explicateur a inclus l'une des caractéristiques aléatoires dans les 5 caractéristiques les plus importantes. Nous observons que dans l'ensemble, nous ne constatons pas d'augmentation systématique de ces pourcentages entre 𝜆 = 0,0 (un MLP de référence sans notre perte de consensus) et 𝜆 = 0,5 (un MLP entraîné avec notre perte de consensus)

\

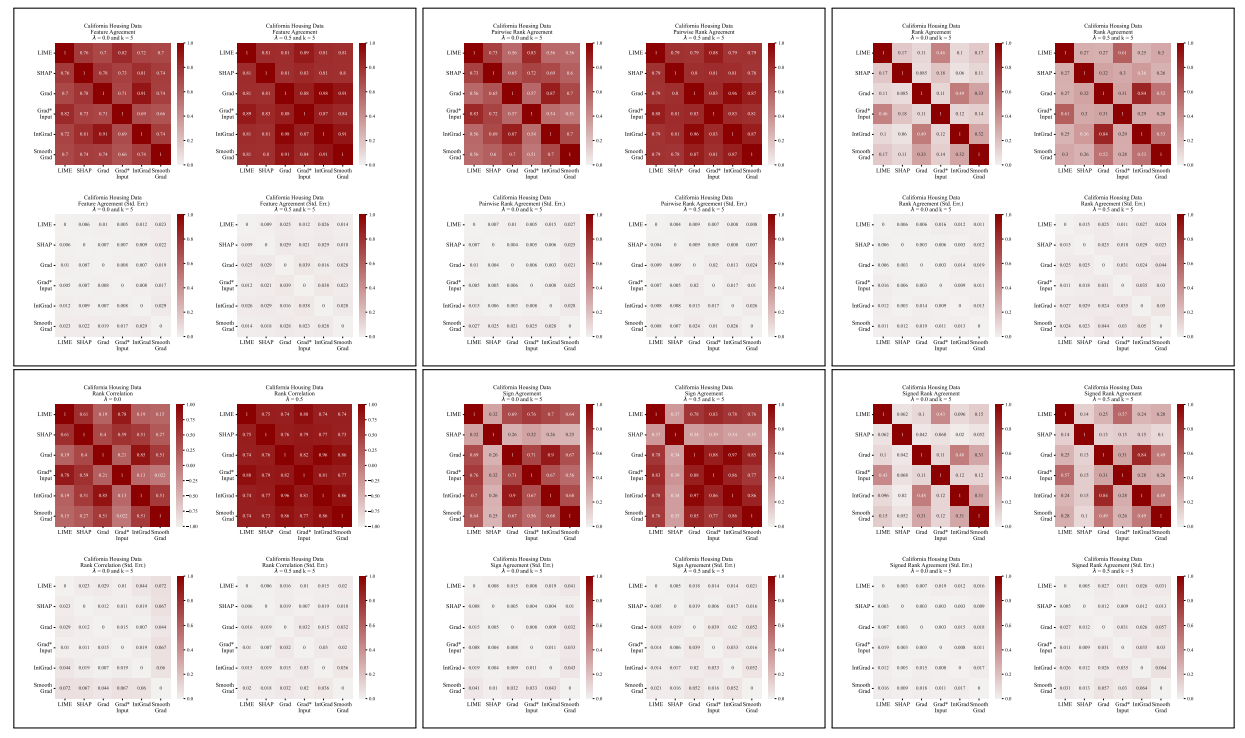
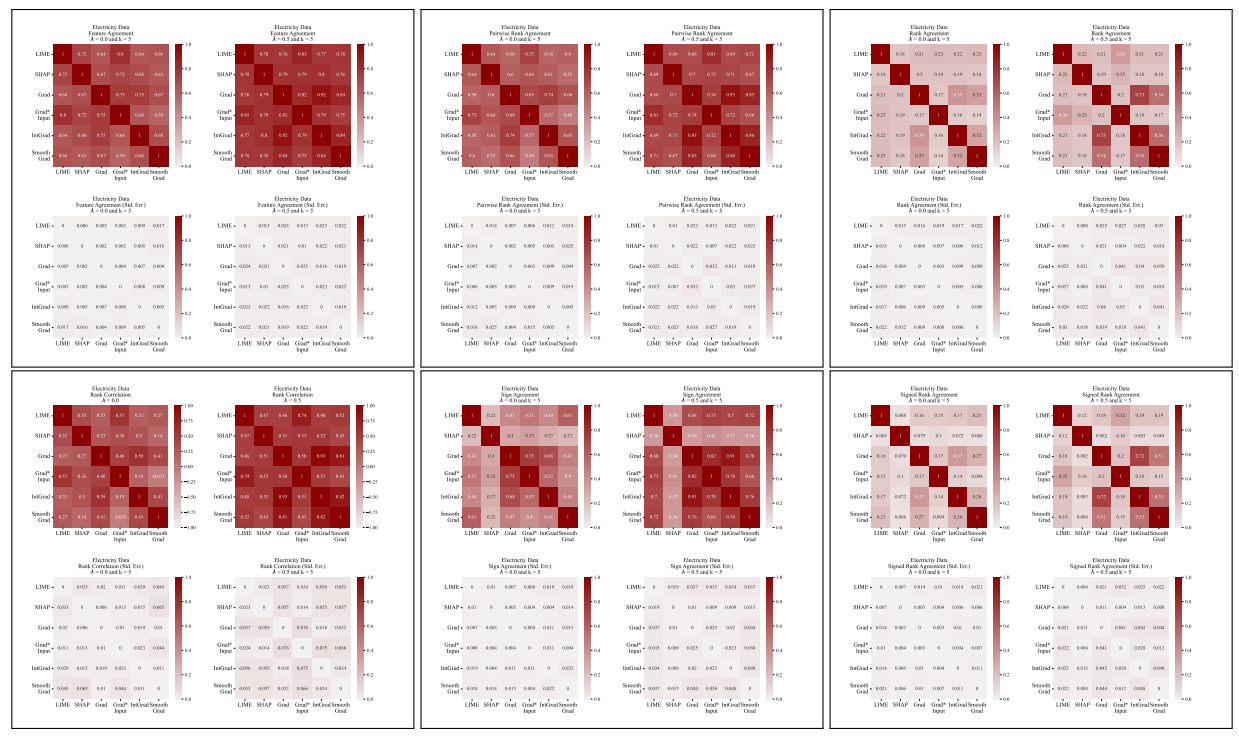
A.5 Plus de matrices de désaccord

\

\

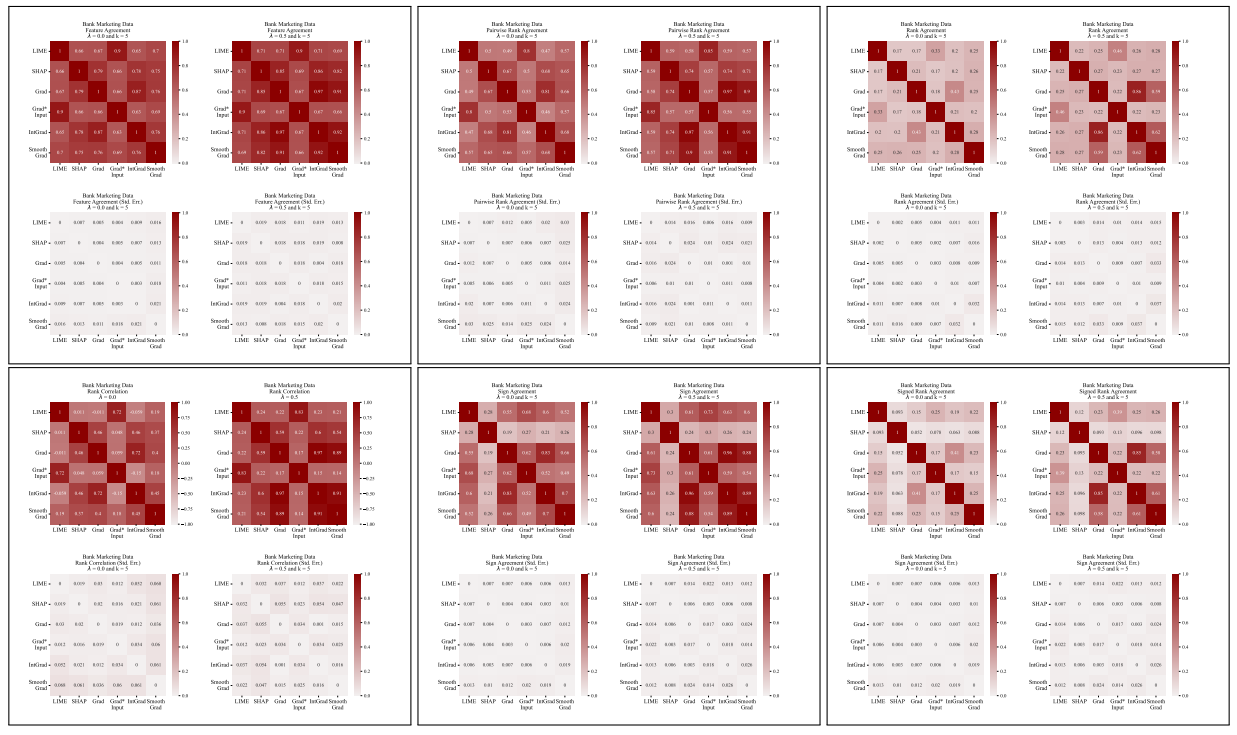
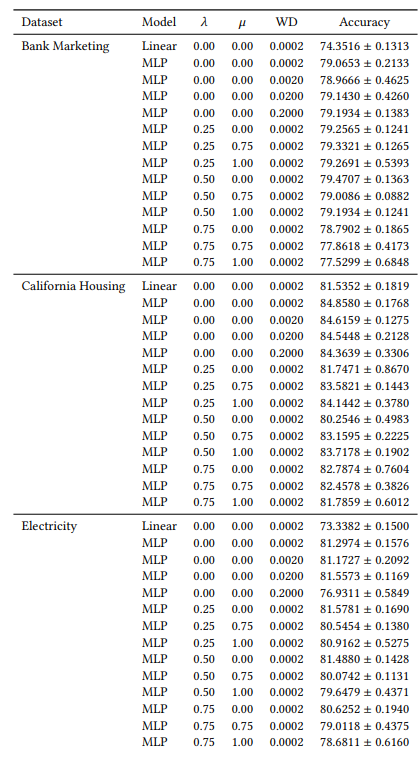
A.6 Résultats étendus

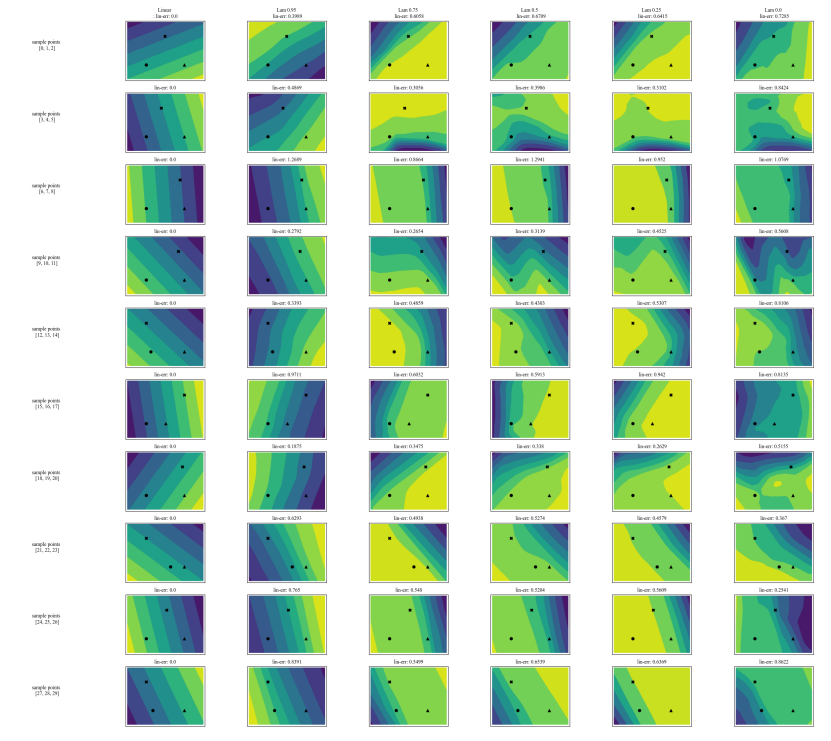
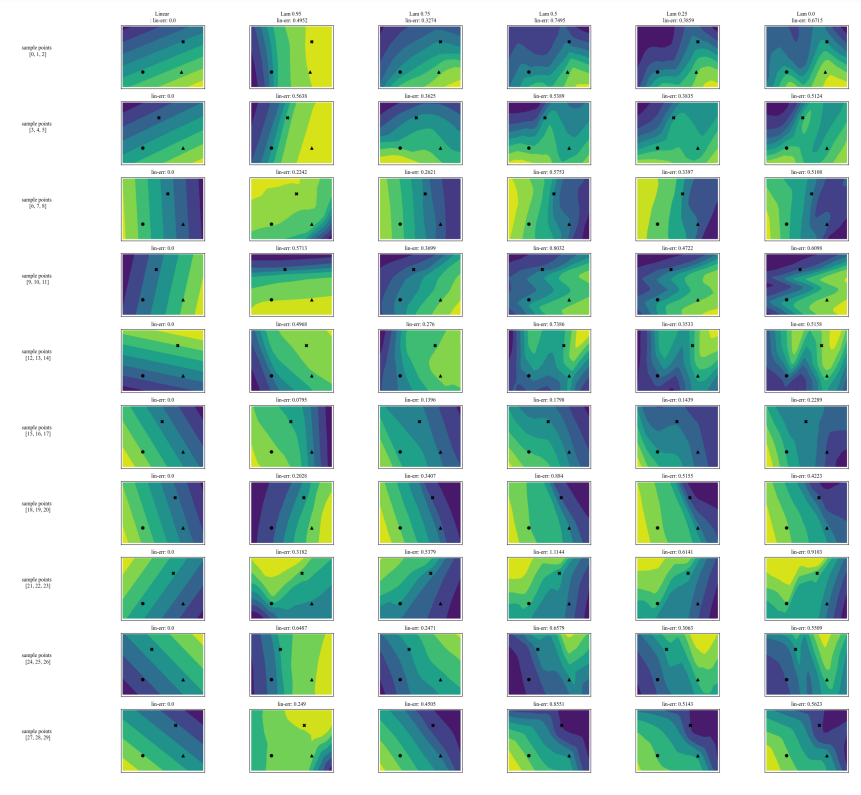
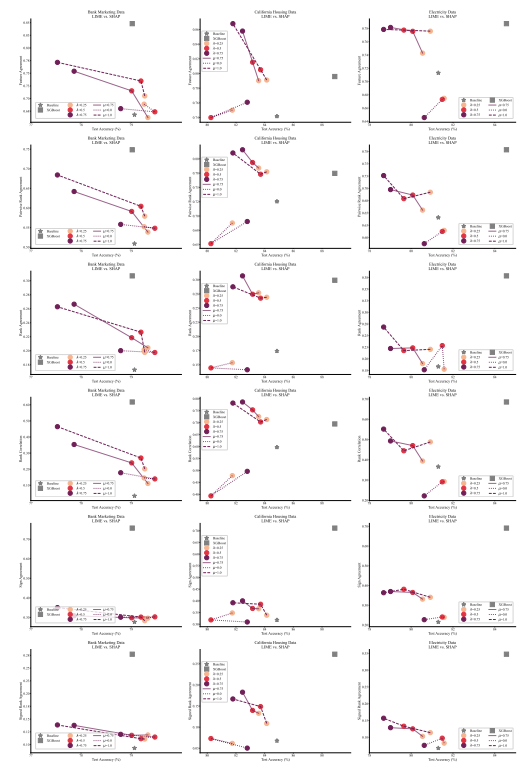
A.7 Graphiques supplémentaires

\

\

\

\

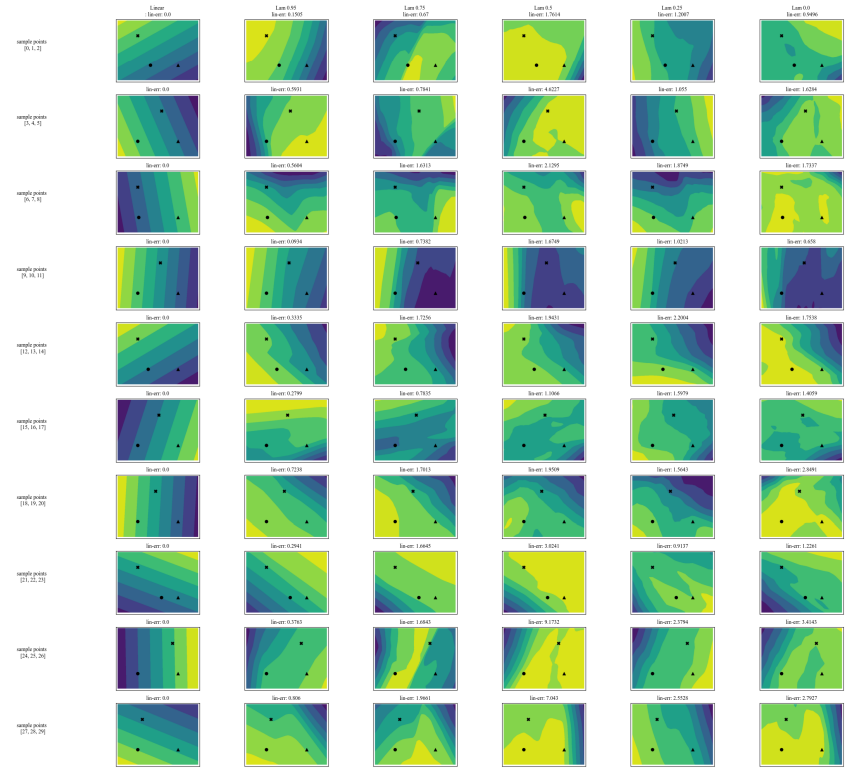
:::info Auteurs :

(1) Avi Schwarzschild, Université du Maryland, College Park, Maryland, USA et travail réalisé en travaillant chez Arthur (avi1umd.edu) ;

(2) Max Cembalest, Arthur, New York City, New York, USA ;

(3) Karthik Rao, Arthur, New York City, New York, USA ;

(4) Keegan Hines, Arthur, New York City, New York, USA ;

(5) John Dickerson†, Arthur, New York City, New York, USA ([email protected]).

:::

:::info Cet article est disponible sur arxiv sous licence CC BY 4.0 DEED.

:::

\