Comment WormHole accélère la recherche de chemins dans les graphes à un milliard d'arêtes

Table des Liens

Abstrait et 1. Introduction

1.1 Notre Contribution

1.2 Cadre

1.3 L'algorithme

1. Travaux Connexes

2. Algorithme

   3.1 La Phase de Décomposition Structurelle

   3.2 La Phase de Routage

   3.3 Variantes de WormHole

3. Analyse Théorique

   4.1 Préliminaires

   4.2 Sous-linéarité de l'Anneau Intérieur

   4.3 Erreur d'Approximation

   4.4 Complexité des Requêtes

4. Résultats Expérimentaux

   5.1 WormHole𝐸, WormHole𝐻 et BiBFS

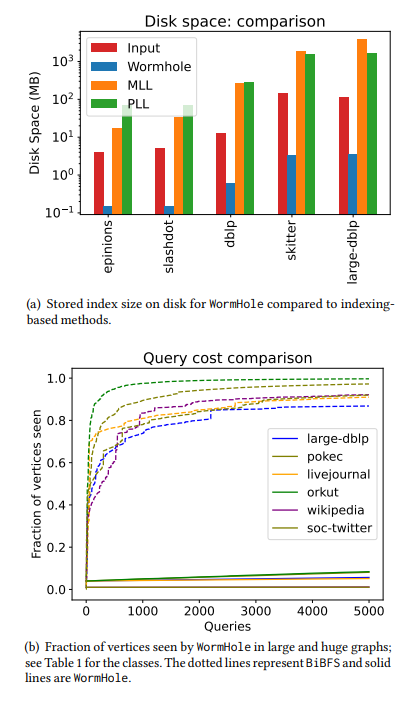
   5.2 Comparaison avec les méthodes basées sur l'indexation

   5.3 WormHole comme primitive : WormHole𝑀

Références

1.1 Notre Contribution

Nous concevons un nouvel algorithme, WormHole, qui crée une structure de données nous permettant de répondre à de multiples requêtes de plus courts chemins en exploitant la structure typique de nombreux réseaux sociaux et d'information. WormHole est simple, facile à implémenter et théoriquement fondé. Nous proposons plusieurs variantes, chacune adaptée à un contexte différent, montrant d'excellents résultats empiriques sur une variété de jeux de données de réseaux. Voici quelques-unes de ses caractéristiques clés :

\ • Compromis performance-précision. À notre connaissance, le nôtre est le premier algorithme sous-linéaire approximatif de plus courts chemins dans les grands réseaux. Le fait que nous autorisions une petite erreur additive donne lieu à un compromis entre le temps/espace de prétraitement et le temps par requête, et nous permet d'aboutir

\

\ à une solution avec un prétraitement efficace et un temps rapide par requête. Notamment, notre variante la plus précise (mais la plus lente), WormHole𝐸, a une précision quasi parfaite : plus de 90% des requêtes sont traitées sans erreur additive, et dans tous les réseaux, plus de 99% des requêtes sont traitées avec une erreur additive d'au plus 2. Voir le Tableau 3 pour plus de détails.

\ • Temps de configuration extrêmement rapide. Notre temps de construction d'index le plus long n'était que de deux minutes, même pour des graphes d'un milliard d'arêtes. Pour contextualiser, PLL et MLL ont expiré sur la moitié des réseaux que nous avons testés, et pour les graphes de taille modérée où PLL et MLL ont terminé leurs exécutions, la construction d'index de WormHole était 100 fois plus rapide. À savoir, WormHole a terminé en quelques secondes tandis que PLL a pris des heures. Voir les Tableaux 4 et 5. Ce temps de configuration rapide est obtenu grâce à l'utilisation d'un index de taille sous-linéaire. Pour les plus grands réseaux que nous avons considérés, il suffit de prendre un index d'environ 1% des nœuds pour obtenir une petite erreur additive moyenne – voir le Tableau 1. Pour les réseaux plus petits, cela peut aller jusqu'à 6%.

\ • Temps de requête rapide. Comparé à BiBFS, la version vanilla WormHole𝐸 (sans optimisations basées sur l'index) est 2 fois plus rapide pour presque tous les graphes et plus de 4 fois plus rapide sur les trois plus grands graphes que nous avons testés. Une variante simple, WormHole𝐻, réalise une amélioration d'un ordre de grandeur au prix d'une certaine précision : systématiquement 20 fois plus rapide sur presque tous les graphes, et plus de 180 fois pour le plus grand graphe que nous avons. Voir le Tableau 3 pour une comparaison complète. Les méthodes basées sur l'indexation répondent généralement aux requêtes en microsecondes ; les deux variantes susmentionnées sont encore dans le régime des millisecondes.

\ • Combinaison de WormHole et de l'état de l'art. WormHole fonctionne en stockant un petit sous-ensemble de sommets sur lesquels nous calculons les chemins les plus courts exacts. Pour des requêtes arbitraires, nous acheminons notre chemin à travers ce sous-ensemble, que nous appelons le noyau. Nous utilisons cette idée pour fournir une troisième variante, WormHole𝑀, en implémentant l'état de l'art pour les plus courts chemins, MLL, sur le noyau. Cela permet d'obtenir des temps de requête comparables à MLL (avec la même garantie de précision que WormHole𝐻) à une fraction du coût de configuration, et fonctionne pour des graphes massifs où MLL ne se termine pas. Nous explorons cette approche combinée dans §5.3, et fournissons des statistiques dans le Tableau 6.

\ • Complexité de requête sous-linéaire. La complexité de requête fait référence au nombre de sommets interrogés par l'algorithme. Dans un modèle d'accès à requête limitée où l'interrogation d'un nœud révèle sa liste de voisins (voir §1.2), la complexité de requête de notre algorithme évolue très bien avec le nombre de requêtes de distance / plus court chemin effectuées. Pour répondre à 5000 requêtes approximatives de plus court chemin, notre algorithme n'observe qu'entre 1% et 20% des nœuds pour la plupart des réseaux. En comparaison, BiBFS voit plus de 90% du graphe pour répondre à quelques centaines de requêtes de plus court chemin. Voir les Figures 2 et 5 pour une comparaison.

\ • Garanties prouvables sur l'erreur et la performance. Dans §4, nous prouvons une suite de résultats théoriques complétant et expliquant la performance empirique. Les résultats, énoncés informellement ci-dessous, sont prouvés pour le modèle de graphes aléatoires de Chung-Lu avec une distribution de degré en loi de puissance [15–17].

\ Théorème 1.1 (Informel). Dans un graphe aléatoire de Chung-Lu 𝐺 avec un exposant de loi de puissance 𝛽 ∈ (2,3) sur 𝑛 sommets, WormHole offre les garanties suivantes avec une forte probabilité :

\

\

:::info Auteurs :

(1) Talya Eden, Université Bar-Ilan ([email protected]) ;

(2) Omri Ben-Eliezer, MIT ([email protected]) ;

(3) C. Seshadhri, UC Santa Cruz ([email protected]).

:::

:::info Cet article est disponible sur arxiv sous licence CC BY 4.0.

:::

\