Mapping Prime Factorization onto Palm Jumeirah: A Geometric View of the Elliptic Curve Method
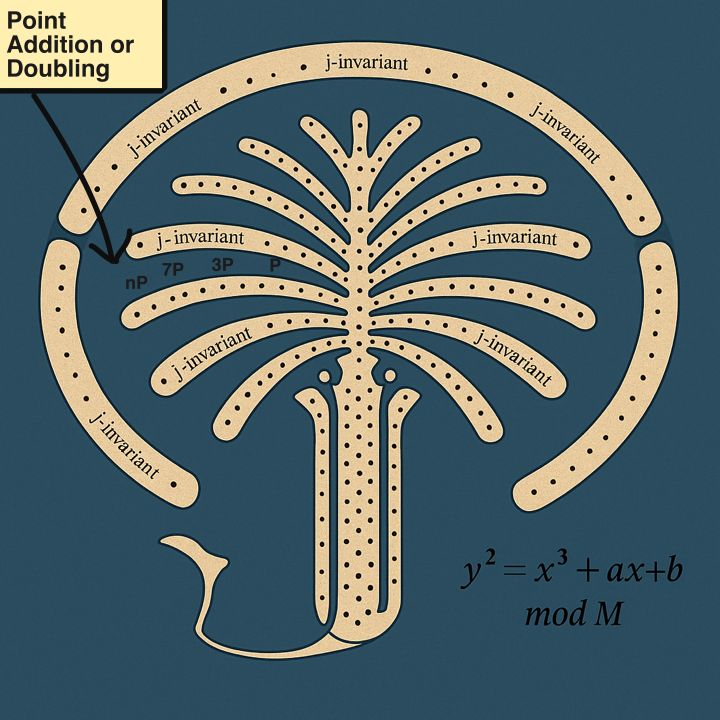
Imagine the Elliptic Curve Method as exploring Palm Jumeirah, Dubai’s iconic palm-shaped island. The island represents an elliptic curve y² = x³ + ax + b mod M, where M is the number to factor (a product of unknown primes). Fronds are j-invariants classifying curve shapes, points (x, y) are coordinates to probe, and the group order (number of points modulo a hidden prime p) is like the frond’s “explorable paths” bounded by Hasse’s theorem: |#E(Fₚ) — (p+1)| ≤ 2√p.
This article uses the Palm Jumeirah Island intuition to explain the Elliptic Curve Method (ECM) for prime factorization. The process starts by finding small treasures (small prime factors) through trial division, then continues along fronds with smooth group orders, forming the mathematical and geometric landscape of the Palm Jumeirah Island model.
Why Palm Jumeirah Island Analogy?
The Palm Jumeirah Island analogy provides a geometric framework for interpreting the abstract mathematics of the Elliptic Curve Method (ECM). By translating algebraic operations into a visually structured, curved-shaped representation, this approach enhances conceptual understanding of the underlying elliptic geometry. It shows how algebraic operations over finite fields can be represented as geometric patterns, creating an intuitive link between number theory and geometry.
Visualizing Complexity
The ECM’s elliptic curves are complex and challenging to visualize. However, they carry out essential calculations to produce factored numbers from a large modulus (M). These numbers are critical for secure cryptographic processes. The shape of the Palm Jumeirah Island curve helps illustrate how these curves can be visualized using Elliptic Curve algebraic equations. This creates a set of points that can be arranged in a palm shape.
Structured Exploration
The frond-shaped layout of Palm Jumeirah Island reflects the organized and systematic nature of the Elliptic Curve Method (ECM). Each frond represents a structured path of exploration — much like the sequential point operations used in ECM to reveal hidden prime factors. In the following section, we examine this process step by step, tracing how points on a fixed elliptic curve are utilized to factor large composite numbers with precision and efficiency.
What is the j-invariant, and how can it be visualized as a Palm Island’s Frond?
In the Elliptic Curve Method (ECM), we explore an elliptic curve defined by a Weierstrass equation (y² = x³ + ax + b (mod M)), where M is a composite number. The curve forms a structured algebraic space over a finite field, populated with points (x, y). To uncover prime factors, ECM seeks curves whose group order modulo a prime factor p is B-smooth — that is, divisible only by small primes up to a bound B.
The j-invariant classifies elliptic curves up to isomorphism class, guiding the search toward curves more likely to yield factors.

\ In the function computeJInvariant, this value is calculated to characterize the curve’s isomorphism class, defining its unique geometric structure.
https://gist.github.com/Deeptiman/464ab7c3bbc54859d719609989cce818?embedable=true
In the function InitializeWeierstrassCurve, trivial j-invariants (j=0 or j=1728) are filtered out during curve initialization, as these correspond to curves with complex multiplication — typically less likely to possess B-smooth group orders. This filtering step ensures that only curves with favorable structures are selected, allowing point operations in GetFactorByECM to proceed efficiently in the search for non-trivial factors.
https://gist.github.com/Deeptiman/835397d55618fd407bea1008755d6d94?embedable=true#file-initializeweierstrasscurve-go
https://gist.github.com/Deeptiman/c94170432a34bcbd2f3b657fd55f757a?embedable=true#file-getfactorby_ecm-go
In the Palm Jumeirah Island analogy, each frond represents a j-invariant — an individual section of the island with its own unique shape. Selecting a frond is analogous to choosing a curve with a non-trivial j-invariant, guiding the search toward fertile regions where coordinates (x, y) are most likely to reveal hidden treasures, or prime factors. The systematic arrangement of the fronds mirrors ECM’s curve selection process, transforming this mathematical procedure into an intuitive and visually engaging exploration across the island’s structured landscape.

\
Mathematical Foundation
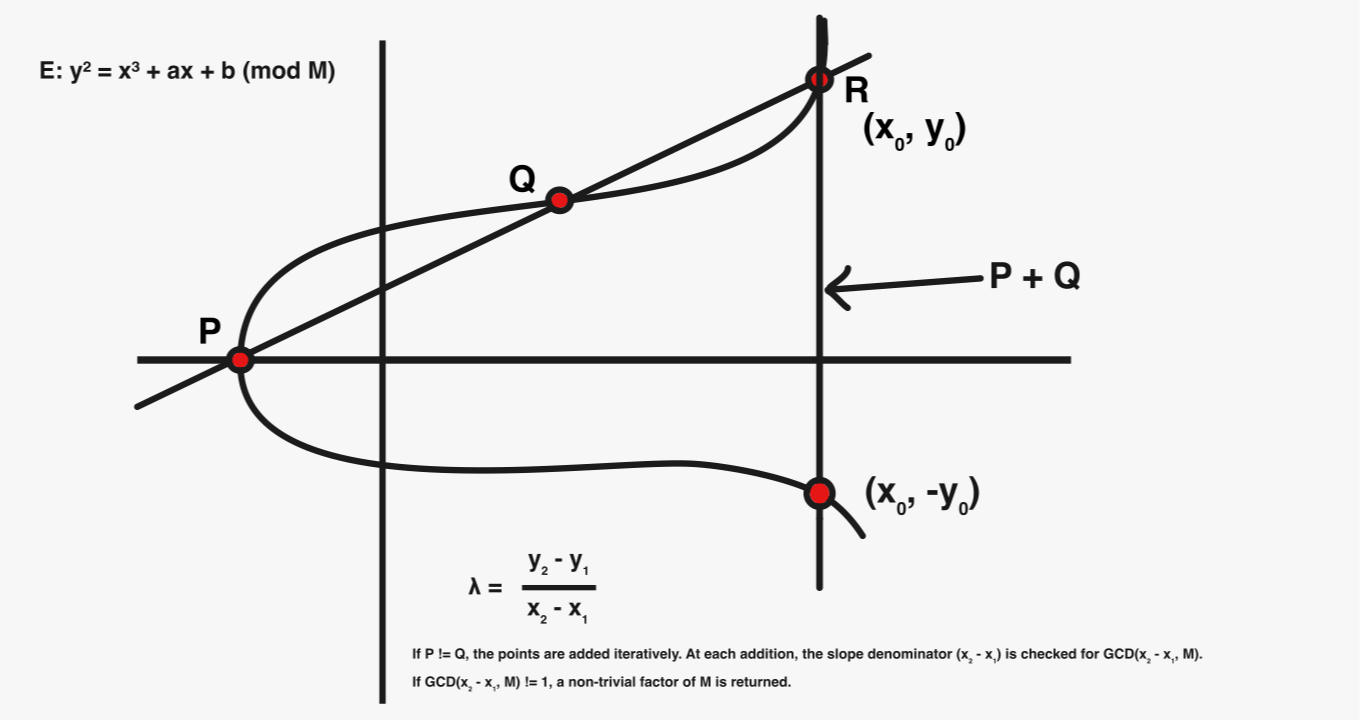
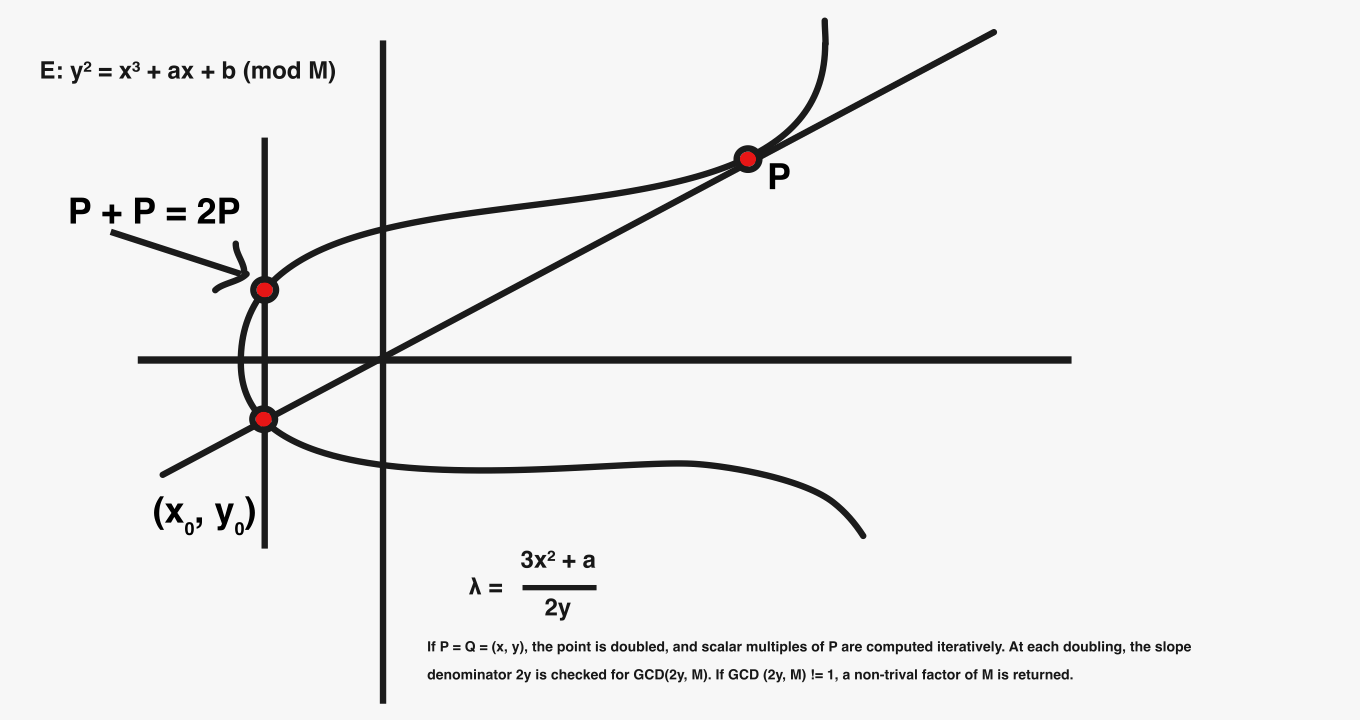
\ These operations, implemented in WithTorsionPoints, which check multiples up to 12 points and within the B-loop of GetFactorByECM, systematically probe the curve’s coordinates to uncover the non-trivial factors. Each iteration performs point addition or doubling that gradually traverses the curve, moving closer to the discovery of hidden factors.
In the Palm Jumeirah Island analogy, the group order is the frond’s area, indicating how many coordinates we can explore. The isomorphism class shapes each frond’s unique geometry, determining its fertility for factor discovery. The pebbles — representing the Frobenius endomorphism — line the fronds’ edges, guiding the sequence of point doublings and additions. Step by step, this structured path leads across the island, revealing the hidden treasure in the form of prime factors uncovered through the factorization process.
\ 
\ 
https://gist.github.com/Deeptiman/3c0b11a0809e08cff3e88fa58270d665?embedable=true#file-point_add-go
\
Uncovering Small Treasures: Trial Division
In the Elliptic Curve Method (ECM), the treasure hunt on Palm Jumeirah Island begins by uncovering small treasures, the prime factors of the composite number M. Using trial division, small primes are tested up to a predefined bound (for example, 10,000) to identify factors such as 2, 7, 73, or 262657. In the function, PreComputedPrimes generates these primes using the Sieve of Eratosthenes, while SmallFactors divides them out of M, reducing the modulus to a smaller and more manageable value for the elliptic curve phase.
This initial step is essential; each small prime factor represents an early treasure retrieved from the island. By collecting these smaller treasures (or prime factors) first, we narrow our search space — focusing the exploration on specific fronds’ coordinates. Tracking unique factors ensures that all discovered divisors are recorded, allowing the algorithm to proceed efficiently towards identifying larger non-trivial factors that remain within the composite modulus.
https://gist.github.com/Deeptiman/42454f7851bc0c41ff16499cbeedc2af?embedable=true#file-precomputeprimes-go
\
Why Sieve of Eratosthenes?
The Sieve of Eratosthenes is a fast algorithm that identifies all primes up to a given number by iteratively marking as non-prime the multiples of each prime, starting from 2 and proceeding up to the given max number. In the function, PreComputePrimes creates a boolean array up to MaxSmallPrime (for example, 10,000), marks non-primes, and collects the remaining primes.
O(n log log n) efficient
It’s highly efficient, generating a set of primes up to max numbers (10,000, 1,000,000) in non-linear time, far faster than testing each number for primality individually. In the Palm Jumeirah Island analogy, the Sieve of Eratosthenes is like crafting a treasure map, marking all possible small prime locations across the island.
Probing Key Coordinates With Torsion Check
On each frond, key coordinates are examined by testing torsion points. In the function, WithTorsionPoints computes (nP) for (n = 2 up to 12), evaluating the greatest common divisor (GCD) of denominators in PointAdd. A curve with a B-smooth point count reveals non-trivial factors quickly, acting like prominent landmarks on the frond.
Explanation:
- Torsion Pre-check: Compute nP for small n (2 < n < 12) first. These are low-cost probes for curves with torsion subgroups. If a denominator during addition yields GCD(denom, M) > 1 (but < M), that’s our factor.
- Phase 1: Accumulate kP where k is the least common multiple of numbers up to B1 (for example, B1 = 10⁶ for medium factors). This covers many small prime powers and utilizes efficient scalar multiplication to avoid naive looping.
- Phase 2: From the Phase 1 result Q, extend by considering primes between B1 and B2 (for example, B2 = 100 * B1).
In the Palm Jumeirah analogy, the torsion check is akin to scouting the base landmarks of the frond. Phase 1 traverses the main path, and Phase 2 explores side branches for hidden treasures.
\ By probing these coordinates, the algorithm rapidly determines if the fronds’ area is fertile, indicating a curve suitable for factor discovery. If no factors are found, explorations continue into additional coordinates in the B-loop. In practice, torsion checks significantly improve computational efficiency, serving as an essential preprocessing step for identifying curves with favourable group order.
\
https://gist.github.com/Deeptiman/ae75c68195bcfb255038879be79bc04a?embedable=true#file-withtorsionpoints-go
\
Try it yourself:
https://go.dev/play/p/2z7mCw96lct
\
Conclusion: Demystifying ECM Through Geometric Intuition: The Palm Jumeirah Framework
Prime factorization mathematics involves complex algebraic structures, such as elliptic curves and their point operations, which can be challenging to visualize. The Palm Jumeirah Island analogy demystifies this complexity by mapping the Elliptic Curve Method (ECM) core elements to a tangible landmark: fronds as j-invariant isomorphism classes, paths as point additions/doublings, and frond areas as B-smooth group orders bounded by Hasse’s theorem.
In this framework, the island’s fronds represent distinct curve shapes, the coordinates correspond to points probed for potential factors, and the frond’s area reflects the underlying group order that governs the search. This visualization makes ECM accessible not only to cryptography experts but also to readers encountering elliptic curve concepts for the first time.
I hope this article provides an understanding of ECM and its cryptographic significance through the visual narrative of the Palm Jumeirah’s geometry. Many other geometric structures exist in the real world, illuminating cryptographic concepts, inviting exploration of mathematical foundations, and their role in building secure systems.
References
- https://wstein.org/edu/124/lenstra/lenstra.pdf
- https://fse.studenttheses.ub.rug.nl/21605/1/bMATH_2020_VisserJ.pdf
- https://crypto.stanford.edu/pbc/notes/elliptic/weier.html
- https://www.youtube.com/watch?v=RAfPy3mRWKA
- https://en.wikipedia.org/wiki/Lenstra_elliptic-curve_factorization
\
You May Also Like

Top Altcoins To Buy Before The ETF Season Kicks In

Token Unlock Wave Highlights Supply Overhang for Traders
