The Math Behind Blockchain Scheduling and Transaction Fee Mechanisms
Table of Links
Abstract and 1. Introduction
1.1 Our Approach
1.2 Our Results & Roadmap
1.3 Related Work
-
Model and Warmup and 2.1 Blockchain Model
2.2 The Miner
2.3 Game Model
2.4 Warm Up: The Greedy Allocation Function
-
The Deterministic Case and 3.1 Deterministic Upper Bound
3.2 The Immediacy-Biased Class Of Allocation Function
-
The Randomized Case
-
Discussion and References
- A. Missing Proofs for Sections 2, 3
- B. Missing Proofs for Section 4
- C. Glossary
\
A: Missing Proofs for Sections 2, 3
\ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
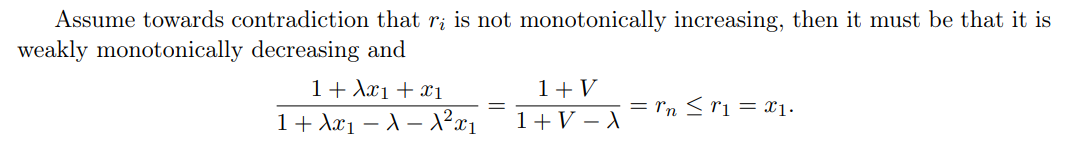
\ \ We now note that a few facts that hold true for any n when x1 ≥ ℓ + ϵ:
\ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
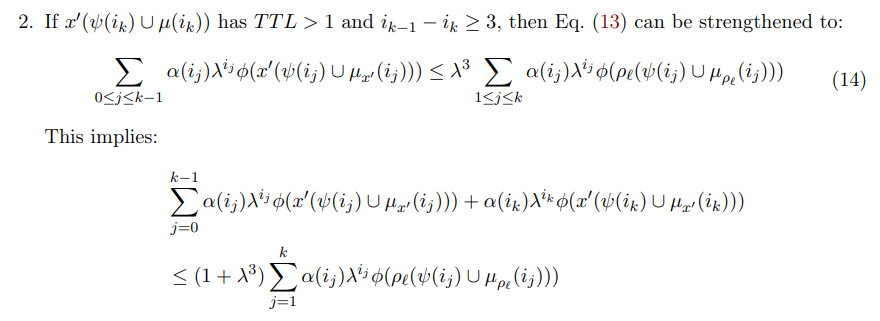
\ \ We separate to several subcases:
\ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \
B Missing Proofs for Section 4
\ We now compare ALG and ADV ’s performance in different steps along the adversary schedule, separating the steps before n and the last two steps.
\ Step i < n.
\ ALG expected performance:
\ 
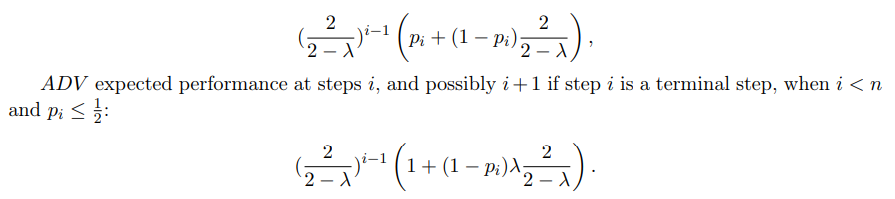
\ Notice that this amortization of considering the i + 1 is only relevant for ADV, as ALG in such case necessarily has no transactions remaining to choose from at step i + 1.
\ 
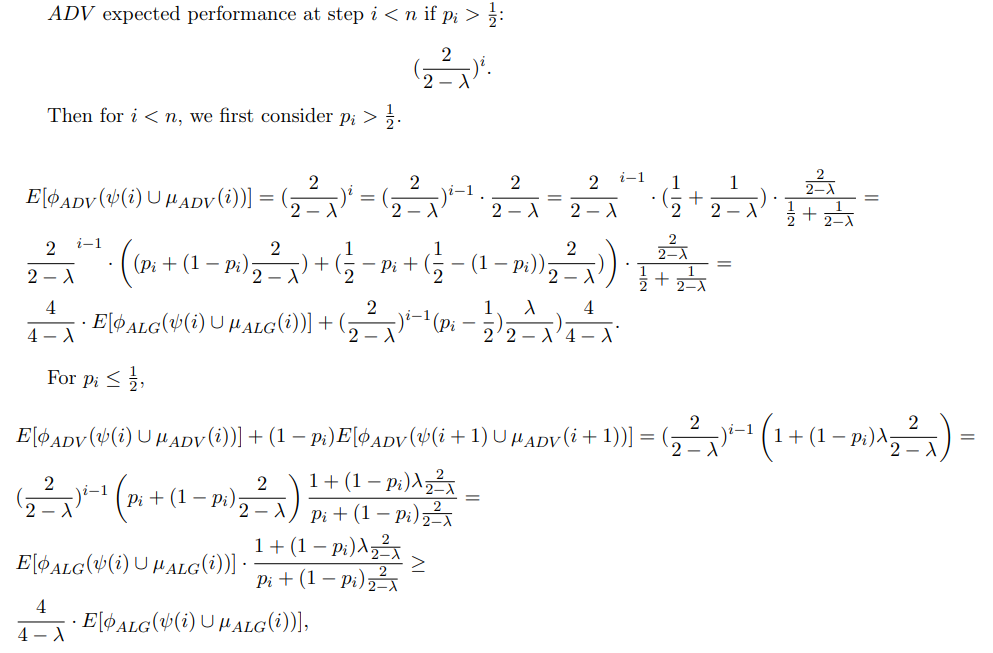
\ where the last transition is since for any 0 ≤ λ ≤ 1, the expression
\ 
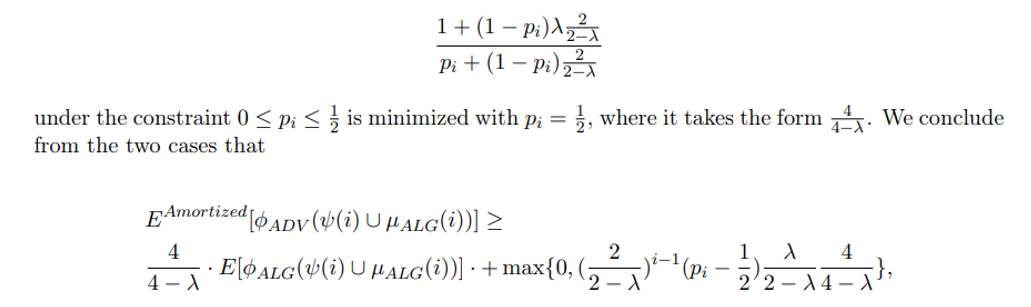
\ We now move on to analyze steps n, n + 1.
\ ALG expected performance at step n, n + 1:
\ 
\ As the base case, consider k = n. Then,
\ 
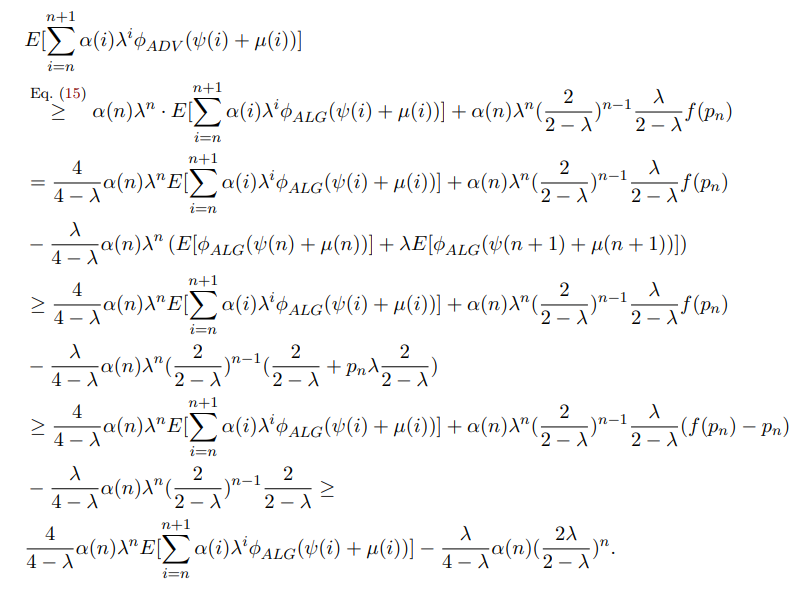
\ For the inductive step,
\ 
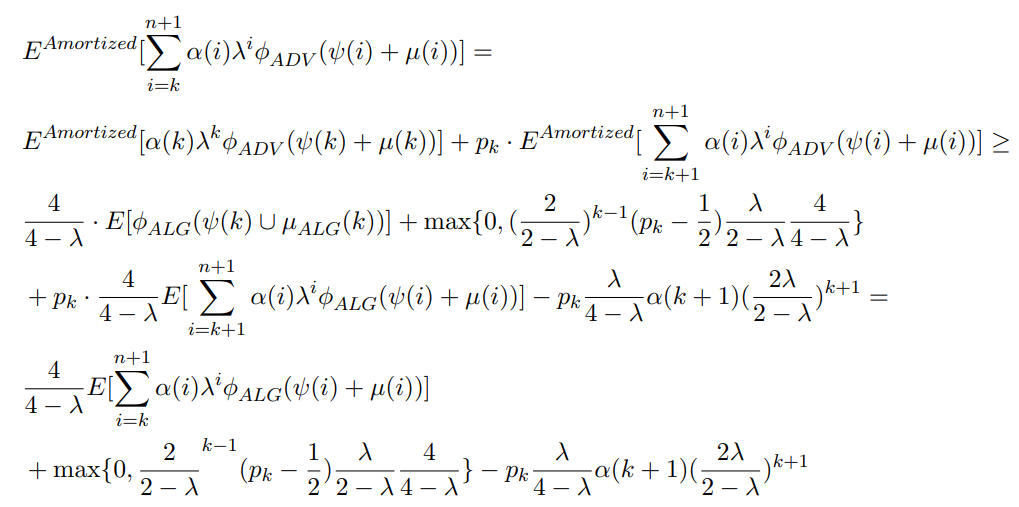
\ We thus need to show that
\ 
\ 
\ 
\ 
\ 
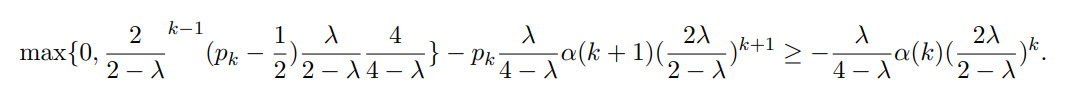
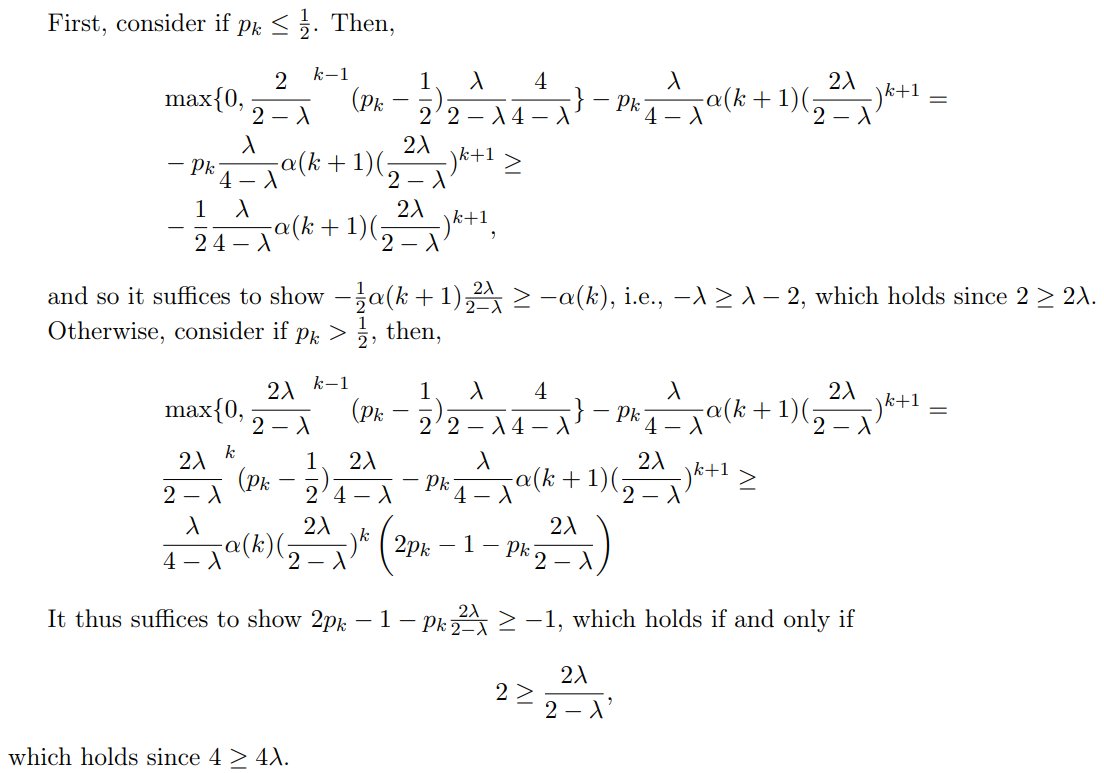
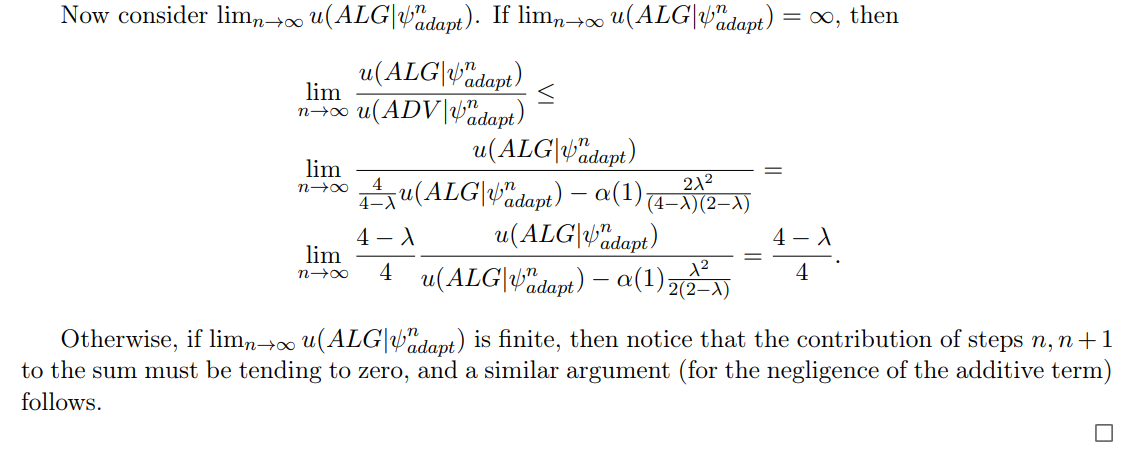
\ With this potential function, we can thus write at step i,
\ 
\
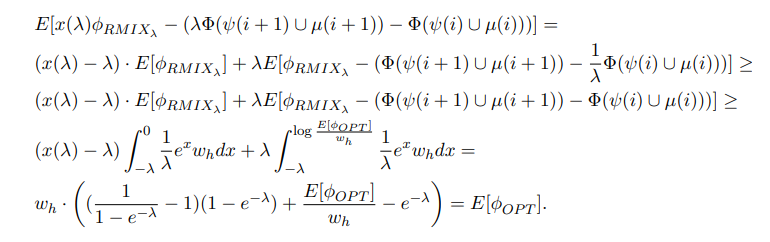
C Glossary
A summary of all symbols and acronyms used in the paper.
C.1 Symbols
ψ Transaction schedule function.
\ x Allocation function.
\ B Predefined maximal block-size, in bytes.
\ λ Miner discount factor.
\ ϕ Transaction fee of some transaction, in tokens.
\ T Miner planning horizon.
\ ℓ Immediacy ratio for our non-myopic allocation rule.
\ µ TTL of past transactions.
\ α Miner’s relative mining power, as a fraction. u Miner revenue.
\ t TTL of a transaction.
\ tx A transaction.
C.2 Acronyms
mempool memory pool
\ PoS Proof-of-Stake
\ PoW Proof-of-Work
\ QoS quality of service
\ TFM transaction fee mechanism
\ TTL time to live
\ \
:::info Authors:
(1) Yotam Gafni, Weizmann Institute ([email protected]);
(2) Aviv Yaish, The Hebrew University, Jerusalem ([email protected]).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
[2] The argument of [CCFJST06] is done by showing conditions that hold for any fixed x ∈ [−1, 0], and so they hold for any fixed x ∈ [−λ, 0] as well.
You May Also Like
Surges to weekly high as Pound strengthens
Strategic $500 Million Move Signals Major Crypto Confidence
