Calibração de Dados de Polarização de Rádio: Melhorando a Correlação Entre os Levantamentos CHIME e Dwingeloo

Tabela de Links

Resumo e 1 Introdução

1. Rotação de Faraday e Síntese de Faraday

2. Dados e Instrumentos

   3.1. Pesquisas CHIME e GMIMS e 3.2. CHIME/GMIMS Banda Baixa Norte

   3.3. Observações do Telescópio de Síntese DRAO

   3.4. Fontes de Dados Auxiliares

3. Características do Girino

   4.1. Morfologia em imagens de frequência única

   4.2. Profundidades de Faraday

   4.3. Complexidade de Faraday

   4.4. Ajuste QU

   4.5. Artefactos

4. A Origem do Girino

   5.1. Estrutura de Hidrogénio Neutro

   5.2. Estrutura de Hidrogénio Ionizado

   5.3. Movimentos Próprios de Estrelas Candidatas

   5.4. Profundidade de Faraday e coluna de eletrões

5. Resumo e Perspetivas Futuras

\ APÊNDICE

A. COMPONENTES DE FARADAY RESOLVIDOS E NÃO RESOLVIDOS NA SÍNTESE DE FARADAY

B. RESULTADOS DO AJUSTE QU

\ REFERÊNCIAS

3.1. Pesquisas CHIME e GMIMS

3.2. CHIME/GMIMS Banda Baixa Norte

\

\ Os mapas de anéis que utilizamos não têm desconvolução de feixe aplicada. Existem pequenos artefactos na imagem resultantes disto que descrevemos na Secção 4.5, no entanto, a sua presença não é prejudicial para o estudo de estruturas na escala de vários graus, como o girino. Nesta análise, utilizamos o subconjunto de 400 − 729 MHz da banda completa CHIME, uma vez que as frequências mais altas estão contaminadas por aliasing, o que torna os mapas pouco fiáveis na região de interesse.

\ 3.2.1. Calibração do ângulo de polarização

\

\

\

\ Stokes U e V são medidos a partir dos produtos de correlação cruzada. Assumimos que ⟨V ⟩ = 0 do céu em emissão difusa porque a emissão de sincrotrão em ambientes astrofísicos de baixa densidade não produz polarização circular. A fuga entre V e U surge de desvios de fase. Medimos um desvio de fase médio ⟨ψ⟩(δ, ν) em cada declinação e frequência assumindo que ⟨V ⟩ = 0 e calculamos

\

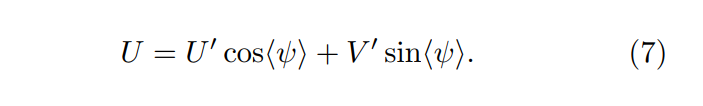
\ A suposição ⟨V ⟩ = 0 leva a ajustes de alta qualidade mesmo em observações de rajadas rápidas de rádio (FRB), onde a suposição tem uma justificação física menos clara do que na emissão polarizada difusa que investigamos (Mckinven et al. 2023). Descobrimos que o desvio de fase é linear em frequência, consistente com um atraso de cabo τ = ⟨ψ⟩/2πν ∼ 1 ns para a emissão difusa, como Mckinven et al. (2021, seu Apêndice A) encontraram nos dados CHIME/FRB.

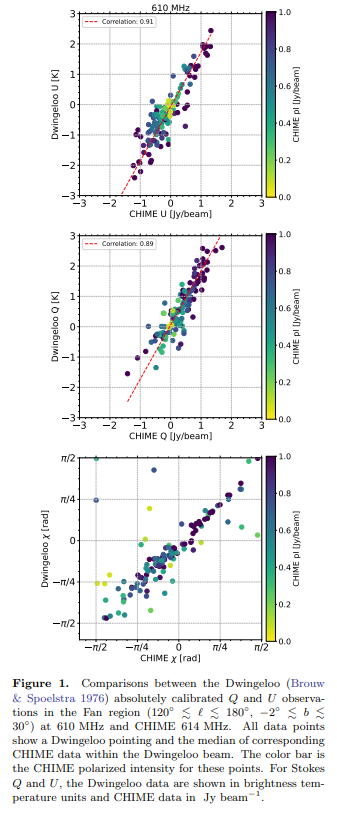
\ Na Figura 1, comparamos os dados calibrados com o levantamento do telescópio Dwingeloo a 610 MHz na região do Fan (Brouw & Spoelstra 1976). Existe uma forte correlação entre Dwingeloo U e CHIME U e Dwingeloo Q e CHIME Q naquelas direções para as quais existem dados Dwingeloo, com valores de coeficiente de correlação R de 0,91 para comparações U − U e 0,89 para comparações Q − Q. Esta é uma melhoria significativa em relação aos coeficientes de correlação não calibrados de 0,76 e 0,59, respetivamente. Encontramos uma fuga remanescente de até 20% em Stokes Q com base em medições de fontes pontuais não resolvidas. Usando a distância ortogonal média entre cada ponto e a linha ajustada, descobrimos que o ruído dos dados CHIME e Dwingeloo descreve ≈ 70% da dispersão na Figura 1. A correlação do ângulo de polarização, também mostrada na Figura 1, também é melhorada através da calibração, e a maioria dos valores discrepantes são pontos com baixa intensidade polarizada (pontos amarelos), onde a incerteza no χ derivado é alta.

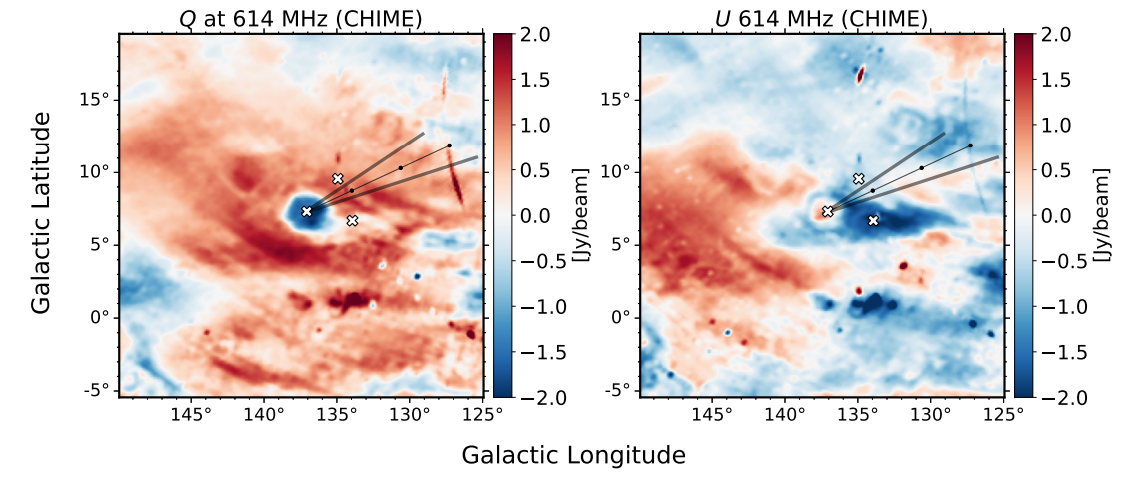
\ Mostramos os mapas CHIME Q e U resultantes, com o eixo de referência χ = 0 rotacionado para o polo galáctico norte, na Figura 2. Embora exista fuga de Stokes I para Q nos nossos dados, a estrutura do girino não pode ser simplesmente o resultado de fuga. Embora haja emissão de intensidade total sobre toda a Região do Fan, incluindo o girino, esta emissão não tem características em pequenas escalas e, portanto, não pode produzir polarização espúria correspondente à morfologia do girino. Além disso, o girino não pode ser o produto da emissão Stokes I originada a grandes distâncias angulares (como o plano galáctico) e vista em lóbulos laterais distantes. Embora os lóbulos laterais distantes tenham propriedades de polarização pobres, sua polarização tem média de valores baixos em áreas consideráveis. Além disso, com alimentações lineares, a fuga de I é principalmente para Q, não U (nas coordenadas equatoriais nativas do CHIME), mas o girino já é evidente em Stokes U em coordenadas equatoriais (não mostrado).

\

\

\ 3.2.2. Síntese de Faraday em dados CHIME

\

\

\ Usando o algoritmo rmtools_peakfitcube em RM-Tools, obtemos o pico de profundidade de Faraday e seu

\

\ erro associado para cada espectro ao longo de todas as linhas de visão. O mapa resultante é mostrado na Figura 3b. Usamos picos de profundidade de Faraday em vez de um primeiro momento (Dickey et al. 2019) para focar na profundidade de Faraday da característica mais brilhante em cada LOS em vez de uma profundidade de Faraday média ponderada em regiões complexas de Faraday.

\ Mostramos a intensidade polarizada integrada através dos espectros de profundidade de Faraday como um mapa de momento zero na Figura 3a. Um mapa de ângulo de polarização desrotacionado para χ0 pelo pico de profundidade de Faraday em cada pixel é mostrado na Figura 3c.

\

:::info Autores:

(1) Nasser Mohammed, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Canada and Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Canada;

(2) Anna Ordog, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Canada and Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Canada;

(3) Rebecca A. Booth, Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Canada;

(4) Andrea Bracco, INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy and Laboratoire de Physique de l'Ecole Normale Superieure, ENS, Universit´e PSL, CNRS, Sorbonne Universite, Universite de Paris, F-75005 Paris, France;

(5) Jo-Anne C. Brown, Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Canada;

(6) Ettore Carretti, INAF-Istituto di Radioastronomia, Via Gobetti 101, 40129 Bologna, Italy;

(7) John M. Dickey, School of Natural Sciences, University of Tasmania, Hobart, Tas 7000 Australia;

(8) Simon Foreman, Department of Physics, Arizona State University, Tempe, AZ 85287, USA;

(9) Mark Halpern, Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1 Canada;

(10) Marijke Haverkorn, Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands;

(11) Alex S. Hill, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Canada and Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Canada;

(12) Gary Hinshaw, Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1 Canada;

(13) Joseph W. Kania, Department of Physics and Astronomy, West Virginia University, P.O. Box 6315, Morgantown, WV 26506, USA and Center for Gravitational Waves and Cosmology, West Virginia University, Chestnut Ridge Research Building, Morgantown, WV 26505, USA;

(14) Roland Kothes, Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Canada;

(15) T.L. Landecker, Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Canada;

(16) Joshua MacEachern, Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1 Canada;

(17) Kiyoshi W. Masui, MIT Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA 02139, USA and Department of Physics, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA 02139, USA