ExchangeDEX+

Comprar cripto Mercados Spot Futuros500X Ganhe Eventos

Mais

Sorteio de Barra de Ouro e BTC2000g

Fractais são padrões infinitos criados pela repetição de equações matemáticas. Vamos desenhar um dos Fractais mais conhecidos, usando apenas JavaScript puro e a API Canvas do HTML5.Fractais são padrões infinitos criados pela repetição de equações matemáticas. Vamos desenhar um dos Fractais mais conhecidos, usando apenas JavaScript puro e a API Canvas do HTML5.

Codificação de uma Árvore Fractal Com JavaScript e HTML5

Por: Hackernoon

2025/10/11 03:00

TREE$0.1184-0.33%

LL$0.007903-0.60%

\ Fractais, essas figuras enigmáticas que estão em todo o lado mas não podem ser vistas pelo olho não treinado. Hoje vamos desenhar um dos Fractais mais conhecidos, usando apenas Vanilla JS e a API Canvas do HTML5. Vamos programar!

O Que Vai Aprender

O que é uma Árvore de Fractal?
Escrever a Árvore de Fractal em Vanilla JS
Além da Árvore de Fractal

O que é uma Árvore de Fractal?

Para definir uma Árvore de Fractal, primeiro, devemos conhecer a definição de Fractal, claro.

Fractais são padrões infinitos criados pela repetição de equações matemáticas, que, em qualquer escala, em qualquer nível de zoom, parecem aproximadamente iguais. Por outras palavras, um objeto geométrico cuja estrutura básica, áspera ou fragmentada, se repete em diferentes escalas.

Então, se dividirmos um Fractal, veremos uma cópia reduzida do todo.

Benoit Mandelbrot, que cunhou o termo Fractal em 1975, disse:

\ Bem claro, certo?

Aqui estão alguns exemplos:

Animated Von Koch Curve

\ Animated Sierpinski Carpet

Agora, o que é uma Árvore de Fractal?

Imagine um ramo, e ramos saindo dele, e depois dois ramos saindo de cada ramo, e assim por diante... é assim que uma Árvore de Fractal se parece.

A sua forma vem do triângulo de Sierpinski (ou gaxeta de Sierpinski).

Como pode ver, um torna-se o outro quando se muda o ângulo entre os ramos:

From Sierpinski Triangle to Fractal

Hoje, vamos terminar com uma figura semelhante à forma final desse GIF.

Escrever a Árvore de Fractal em Vanilla JS

Antes de mais nada, aqui está o produto final (pode ajustá-lo ao longo do caminho):

Final Fractal Tree

Agora vamos desenhar isso, passo a passo.

Primeiro, inicializamos o nosso ficheiro index.html com um canvas de dimensões razoáveis e uma tag script onde todo o nosso código JS estará.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script></script>   </body> </html>

Depois, começamos a escrever o nosso JavaScript.

Inicializamos o nosso elemento canvas em JS, acedendo-o através da variável myCanvas e criando o contexto de renderização 2D com a variável ctx (contexto).

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");     </script>   </body> </html>

Então, o método getContext adiciona propriedades e métodos que permitem desenhar, neste caso, em 2D.

Agora é hora de pensar. Como podemos definir o algoritmo para desenhar uma árvore Fractal? Hm... 🤔

Vejamos, sabemos que os ramos continuam a ficar menores. E que cada ramo termina com dois ramos a sair dele, um para a esquerda e outro para a direita.

Por outras palavras, quando um ramo é suficientemente longo, anexe dois ramos menores a ele. Repita.

Parece que devemos usar alguma declaração recursiva em algum lugar, não é?

Voltando ao código, agora definimos a nossa função fractalTree que deve receber pelo menos quatro argumentos: as coordenadas X e Y onde o ramo começa, o comprimento do seu ramo e o seu ângulo.

Dentro da nossa função, começamos o desenho com o método beginPath(), e depois guardamos o estado do canvas com o método save().

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();       }     </script>   </body> </html>

O método beginPath é frequentemente usado quando se inicia uma nova linha ou figura que tem um estilo fixo, como a mesma cor ao longo de toda a linha, ou a mesma largura. O método save apenas guarda o estado inteiro do canvas empurrando o estado atual para uma pilha.

Agora vamos desenhar a nossa Árvore de Fractal desenhando uma linha (ramo), rodando o canvas, desenhando o próximo ramo, e assim por diante. É assim (vou explicar cada método abaixo da amostra de código):

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, -15);           draw(0, -len, len*0.8, +15);            ctx.restore();       }       draw(400, 600, 120, 0)     </script>   </body> </html>

Então primeiro adicionamos três métodos, translate, rotate e moveTo, que "movem" o canvas, a sua origem e o nosso "lápis" para que possamos desenhar o ramo no ângulo desejado. É como se estivéssemos a desenhar um ramo, depois a centrar este ramo (movendo todo o canvas), e depois a desenhar um novo ramo a partir do fim do nosso ramo anterior.

Os últimos dois métodos antes da declaração if são lineTo e stroke; o primeiro adiciona uma linha reta ao caminho atual, e o segundo renderiza-a. Pode pensar assim: lineTo dá a ordem, e stroke executa-a.

Agora temos uma declaração if que diz quando parar a recursão, quando parar de desenhar. O método restore, como indicado nos Docs MDN, "restaura o estado do canvas mais recentemente guardado, retirando a entrada superior na pilha de estado de desenho".

Após a declaração if, temos a chamada recursiva e outra chamada ao método restore. E depois uma chamada à função que acabámos de terminar.

Agora execute o código no seu navegador. Verá, finalmente, uma Árvore de Fractal!

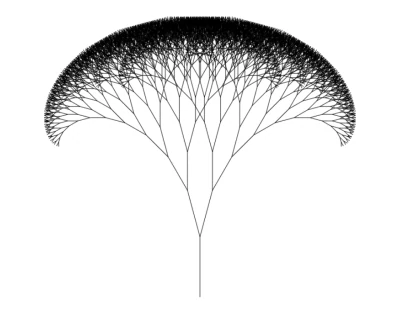
Fractal Tree First Iteration

Incrível, certo? Agora vamos torná-la ainda melhor.

Vamos adicionar um novo parâmetro à nossa função draw, branchWidth, para tornar a nossa Árvore de Fractal mais realista.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Então em cada iteração, estamos a fazer cada ramo mais fino. Também mudei o parâmetro de ângulo na chamada recursiva para fazer uma árvore mais "aberta".

Agora, vamos adicionar alguma cor! E sombras, por que não.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.strokeStyle = "green";           ctx.fillStyle = "green";            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            ctx.shadowBlur = 15;           ctx.shadowColor = "rgba(0,0,0,0.8)";            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Ambos os métodos de cor são autoexplicativos (strokeStyle e fillStyle). Também os de sombra, shadowBlur e shadowColor.

E é isso! Guarde o ficheiro e abra-o com o seu navegador para ver o produto final.

Agora encorajo-o a brincar com o código! Mude o shadowColor, o fillStyle, faça uma Árvore de Fractal mais curta ou mais longa, mude o ângulo, ou tente adicionar folhas, isso deve ser desafiante 😉

Além da Árvore de Fractal

Como mostrei no início deste post, existem diferentes Fractais. Não vai ser fácil fazer todos esses com a API Canvas, mas deve ser possível. Fiz alguns desses na linguagem de programação C, e também brinquei com p5.js.

p5.js é uma biblioteca JavaScript Open Source feita por artistas, para artistas, baseada na linguagem Processing. Pode desenhar ou animar qualquer coisa imaginável. Se estiver interessado em fazer arte com código, é imprescindível. Eles têm uma ótima página de get-started que pode consultar aqui.

Bem, é isso por agora! Obrigado por ler, comente quaisquer perguntas, e vejo-o no meu próximo post!

Isenção de responsabilidade: Os artigos republicados neste site são provenientes de plataformas públicas e são fornecidos apenas para fins informativos. Eles não refletem necessariamente a opinião da MEXC. Todos os direitos permanecem com os autores originais. Se você acredita que algum conteúdo infringe direitos de terceiros, entre em contato pelo e-mail [email protected] para solicitar a remoção. A MEXC não oferece garantias quanto à precisão, integridade ou atualidade das informações e não se responsabiliza por quaisquer ações tomadas com base no conteúdo fornecido. O conteúdo não constitui aconselhamento financeiro, jurídico ou profissional, nem deve ser considerado uma recomendação ou endosso por parte da MEXC.