Понимание ошибки аппроксимации и сложности запросов в маршрутизации WormHole
Таблица ссылок
Резюме и 1. Введение
1.1 Наш вклад
1.2 Настройка
1.3 Алгоритм
-
Связанные работы
-
Алгоритм
3.1 Фаза структурной декомпозиции
3.2 Фаза маршрутизации
3.3 Варианты WormHole
-
Теоретический анализ
4.1 Предварительные сведения
4.2 Сублинейность внутреннего кольца
4.3 Ошибка аппроксимации
4.4 Сложность запросов
-
Экспериментальные результаты
5.1 WormHole𝐸, WormHole𝐻 и BiBFS
5.2 Сравнение с методами на основе индексов
5.3 WormHole как примитив: WormHole𝑀
Ссылки
4.3 Ошибка аппроксимации
Теперь, когда у нас есть сублинейное внутреннее кольцо, содержащее ядро Чунг-Лу, мы должны показать, что маршрутизация путей через него влечет лишь небольшой штраф. Интуитивно понятно, что чем больше внутреннее кольцо, тем легче это удовлетворить: если внутреннее кольцо - это весь граф, утверждение выполняется тривиально. Поэтому задача заключается в том, чтобы показать, что мы можем достичь сильной гарантии в отношении точности даже с сублинейным внутренним кольцом. Мы доказываем, что WormHole влечет аддитивную ошибку не более 𝑂(loglog𝑛) для всех пар, что намного меньше диаметра Θ(log𝑛).
\ 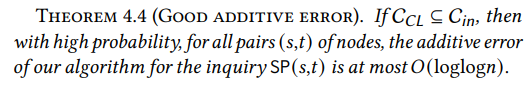
\ Вышеуказанный результат справедлив с высокой вероятностью даже в худшем случае. А именно, для всех пар (𝑠,𝑡) вершин в графе длина пути, возвращаемого WormHole, не более чем на 𝑂(loglog𝑛) превышает фактическое расстояние между 𝑠 и 𝑡. Это тривиально означает, что средняя аддитивная ошибка WormHole с высокой вероятностью ограничена той же величиной.
\ 
\
4.4 Сложность запросов
Вспомним модель запросов узлов в этой статье (см. §1.2): начиная с одного узла, нам разрешено итеративно делать запросы, где каждый запрос извлекает список соседей выбранного нами узла 𝑣. Нас интересует сложность запросов, т.е. количество запросов, необходимых для выполнения определенных операций.
\ \ 
\ \ Первый результат - это верхняя граница нашей производительности.
\ \ 
\ \ Набросок доказательства. Для данного запроса SP(𝑢, 𝑣) мы даем верхнюю границу сложности запросов BFS, который начинается с 𝑢, и аналогично для 𝑣; общая сложность запросов - это сумма этих двух величин.
\ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \
:::info Авторы:
(1) Talya Eden, Университет Бар-Илан ([email protected]);
(2) Omri Ben-Eliezer, MIT ([email protected]);
(3) C. Seshadhri, UC Santa Cruz ([email protected]).
:::
:::info Эта статья доступна на arxiv под лицензией CC BY 4.0.
:::
\
Вам также может быть интересно

GhostSwap легитимен? Полный обзор 2025 года биржи криптовалют, ориентированной на конфиденциальность без KYC

Tether представила конкурента Apple Health с шифрованием и локальным ИИ
