Розуміння похибки апроксимації та складності запитів у маршрутизації WormHole

Таблиця посилань

Анотація та 1. Вступ

1.1 Наш внесок

1.2 Налаштування

1.3 Алгоритм

1. Пов'язані роботи

2. Алгоритм

   3.1 Фаза структурної декомпозиції

   3.2 Фаза маршрутизації

   3.3 Варіанти WormHole

3. Теоретичний аналіз

   4.1 Передумови

   4.2 Сублінійність внутрішнього кільця

   4.3 Похибка апроксимації

   4.4 Складність запиту

4. Експериментальні результати

   5.1 WormHole𝐸, WormHole𝐻 та BiBFS

   5.2 Порівняння з методами на основі індексів

   5.3 WormHole як примітив: WormHole𝑀

Посилання

4.3 Похибка апроксимації

Тепер, коли у нас є сублінійне внутрішнє кільце, що містить ядро Чунг-Лу, ми повинні показати, що маршрутизація шляхів через нього призводить лише до невеликого штрафу. Інтуїтивно зрозуміло, що чим більше внутрішнє кільце, тим легше це задовольнити: якщо внутрішнє кільце є всім графом, твердження виконується тривіально. Тому виклик полягає в тому, щоб показати, що ми можемо досягти сильної гарантії точності навіть із сублінійним внутрішнім кільцем. Ми доводимо, що WormHole призводить до адитивної похибки не більше 𝑂(loglog𝑛) для всіх пар, що значно менше діаметра Θ(log𝑛).

\

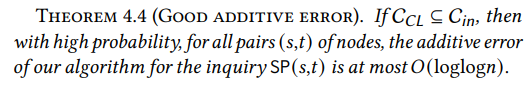
\ Вищезазначений результат виконується з високою ймовірністю навіть у найгіршому випадку. А саме, для всіх пар (𝑠,𝑡) вершин у графі, довжина шляху, поверненого WormHole, щонайбільше на 𝑂(loglog𝑛) перевищує фактичну відстань між 𝑠 та 𝑡. Це тривіально означає, що середня адитивна похибка WormHole з високою ймовірністю обмежена тією ж величиною.

\

\

4.4 Складність запиту

Нагадаємо модель запиту вузла в цій статті (див. §1.2): починаючи з одного вузла, нам дозволено ітеративно робити запити, де кожен запит отримує список сусідів вузла 𝑣 за нашим вибором. Нас цікавить складність запиту, тобто кількість запитів, необхідних для проведення певних операцій.

\ \

\ \ Перший результат - це верхня межа нашої продуктивності.

\ \

\ \ Схема доведення. Для даного запиту SP(𝑢, 𝑣) ми даємо верхню межу складності запиту BFS, що починається з 𝑢, і аналогічно для 𝑣; загальна складність запиту є сумою цих двох величин.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info Автори:

(1) Талья Еден, Університет Бар-Ілан ([email protected]);

(2) Омрі Бен-Еліезер, MIT ([email protected]);

(3) К. Сешадрі, Університет Каліфорнії, Санта-Крус ([email protected]).

:::

:::info Ця стаття доступна на arxiv за ліцензією CC BY 4.0.

:::

\