交易所DEX+

零费率盛典

本文讨论了银河蝌蚪在去旋转偏振角度图中仍然保持为一个独特的、空间均匀特征的令人费解的观察结果。本文讨论了银河蝌蚪在去旋转偏振角度图中仍然保持为一个独特的、空间均匀特征的令人费解的观察结果。

法拉第复杂性的证据：极化角均匀性表明存在多个特征

作者：Hackernoon

来源：Hackernoon

2025/10/10 00:00

链接表

摘要和1 引言

法拉第旋转和法拉第合成
数据和仪器

3.1. CHIME和GMIMS调查以及3.2. CHIME/GMIMS北部低频段

3.3. DRAO合成望远镜观测

3.4. 辅助数据源
蝌蚪的特征

4.1. 单频图像中的形态

4.2. 法拉第深度

4.3. 法拉第复杂性

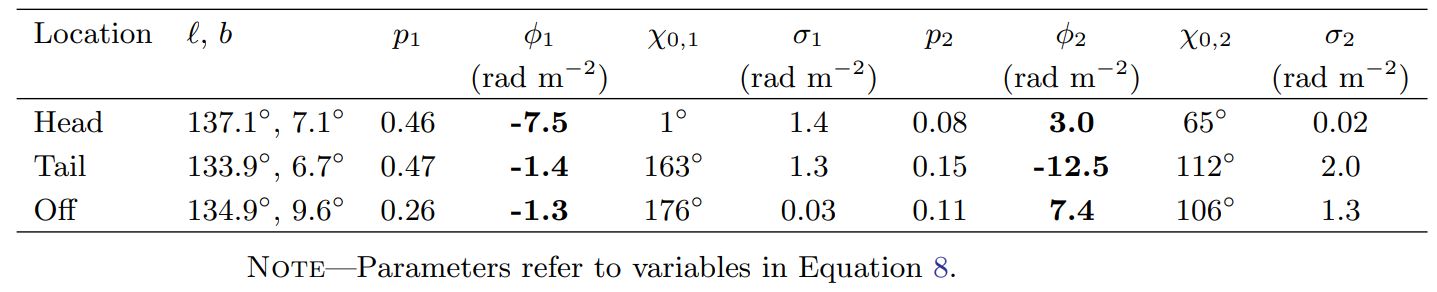
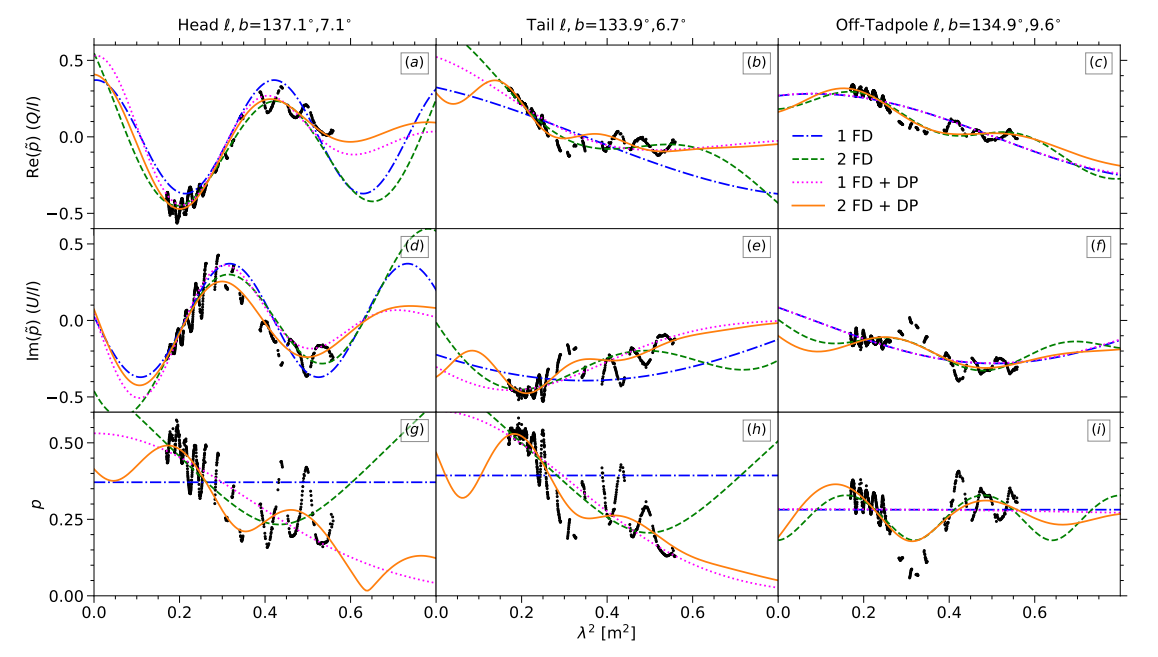
4.4. QU拟合

4.5. 伪影
蝌蚪的起源

5.1. 中性氢结构

5.2. 电离氢结构

5.3. 候选恒星的自行

5.4. 法拉第深度和电子柱密度
总结和未来展望

\ 附录

A. 法拉第合成中的已解析和未解析法拉第成分

B. QU拟合结果

\ 参考文献

4.3. 法拉第复杂性

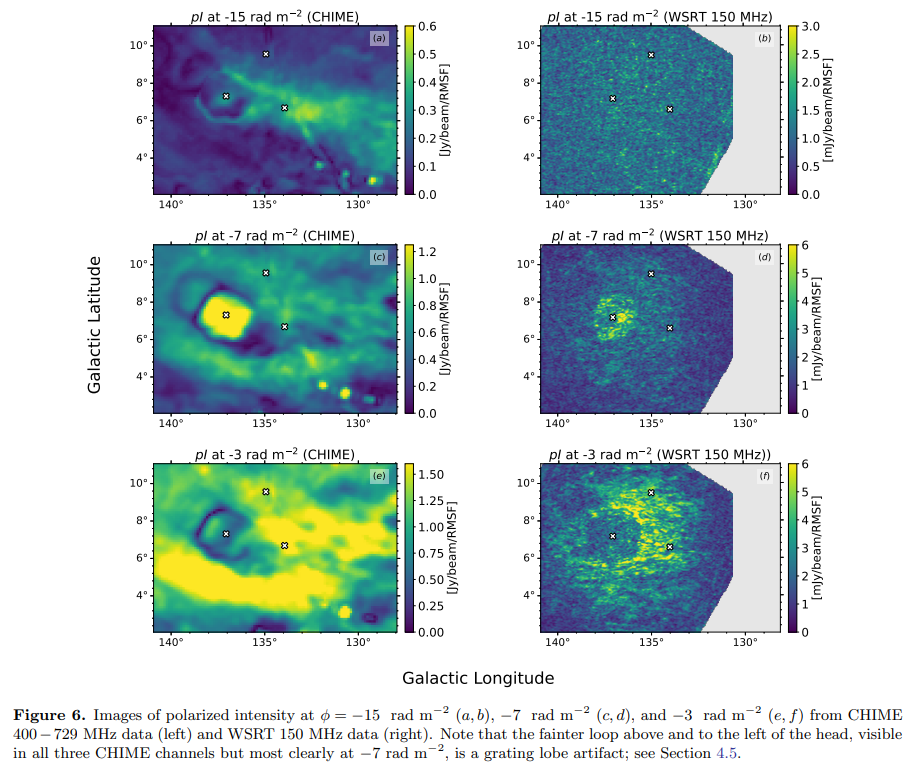
使用图3b中的峰值法拉第深度，我们通过重新排列方程1将观测到的偏振角去旋转至标称本征角。结果如图3c所示，显示尾部是一个独特的特征，与其背景分离，并且在

\ 表2. 代表性视线的QU拟合结果

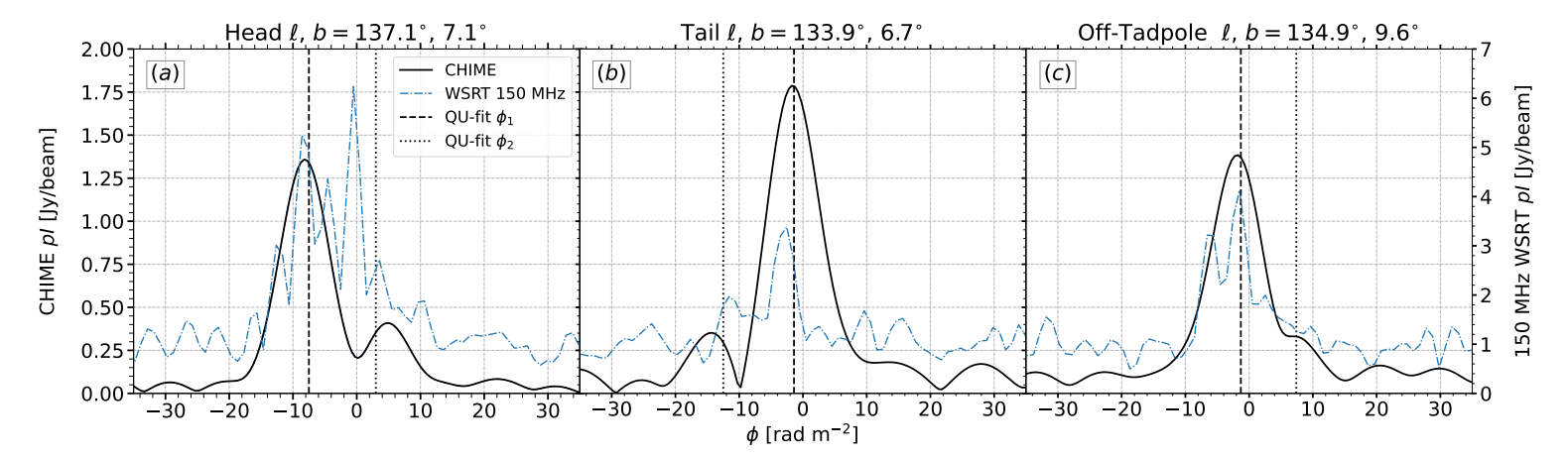
\ 偏振角上空间均匀。如果蝌蚪仅仅是一种法拉第旋转现象，每条视线由单一的法拉第简单特征表示，我们不会期望它在去旋转的χ图中可见。它确实出现的事实意味着，要么蝌蚪贡献了与其周围环境不同的显著偏振辐射，要么沿着穿过它的视线存在法拉第复杂性。后一种可能性由图7中的样本法拉第深度谱和图6中显示的图像切片强烈暗示。

\ 图7. 来自CHIME 400−729 MHz（黑色实线）和WSRT 150 MHz（蓝色点划线）的法拉第谱（幅度），用于蝌蚪头部、尾部和周围区域的视线。这些视线对应于图2和其他地方显示的标记。虚线和点线垂直线显示了来自QU拟合的峰值ϕ1和ϕ2（见4.4节）。左侧的强度刻度适用于CHIME数据；右侧的强度刻度适用于WSRT数据。

\ 图8. 图7所示视线的QU拟合最佳模型。这些面板显示Q/I（a−c）、U/I（d−f）和分数偏振强度p（g−i）。黑点表示数据。蓝色点划线是1组分模型（1 FD），绿色虚线是两组分模型（2 FD），洋红色点线是带波束去偏振的1组分模型（1 FD+DP），橙色实线是带波束去偏振的两组分模型（2 FD+DP）。数据中的快速波纹（一种仪器效应）未被模型拟合。

:::info 作者：

(1) Nasser Mohammed，不列颠哥伦比亚大学奥肯那根校区计算机科学、数学、物理与统计系，加拿大基洛纳BC V1V 1V7和加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248；

(2) Anna Ordog，不列颠哥伦比亚大学奥肯那根校区计算机科学、数学、物理与统计系，加拿大基洛纳BC V1V 1V7和加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248；

(3) Rebecca A. Booth，卡尔加里大学物理和天文系，加拿大艾伯塔省卡尔加里西北大学道2500号，T2N 1N4；

(4) Andrea Bracco，INAF – 阿切特里天体物理天文台，意大利佛罗伦萨E. Fermi大道5号，50125和法国巴黎高等师范学院物理实验室，ENS，巴黎科学文学艺术大学，法国国家科学研究中心，索邦大学，巴黎大学，F-75005；

(5) Jo-Anne C. Brown，卡尔加里大学物理和天文系，加拿大艾伯塔省卡尔加里西北大学道2500号，T2N 1N4；

(6) Ettore Carretti，INAF-射电天文研究所，意大利博洛尼亚Gobetti路101号，40129；

(7) John M. Dickey，塔斯马尼亚大学自然科学学院，澳大利亚霍巴特，Tas 7000；

(8) Simon Foreman，亚利桑那州立大学物理系，美国亚利桑那州坦佩，85287；

(9) Mark Halpern，不列颠哥伦比亚大学物理和天文系，加拿大温哥华BC V6T 1Z1，农业路6224号；

(10) Marijke Haverkorn，拉德堡德大学天体物理学/IMAPP系，荷兰奈梅亨，邮政信箱9010，6500 GL；

(11) Alex S. Hill，不列颠哥伦比亚大学奥肯那根校区计算机科学、数学、物理与统计系，加拿大基洛纳BC V1V 1V7和加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248；

(12) Gary Hinshaw，不列颠哥伦比亚大学物理和天文系，加拿大温哥华BC V6T 1Z1，农业路6224号；

(13) Joseph W. Kania，西弗吉尼亚大学物理和天文系，美国西弗吉尼亚州摩根敦，邮政信箱6315，26506和西弗吉尼亚大学引力波和宇宙学中心，美国西弗吉尼亚州摩根敦，栗树岭研究大楼，26505；

(14) Roland Kothes，加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248；

(15) T.L. Landecker，加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248；

(16) Joshua MacEachern，不列颠哥伦比亚大学物理和天文系，加拿大温哥华BC V6T 1Z1，农业路6224号；

(17) Kiyoshi W. Masui，麻省理工学院卡维里天体物理和空间研究所，美国马萨诸塞州剑桥，马萨诸塞大道77号，02139和麻省理工学院物理系，美国马萨诸塞州剑桥，马萨诸塞大道77号，02139；

(18) Aimee Menard，不列颠哥伦比亚大学奥肯那根校区计算机科学、数学、物理与统计系，加拿大基洛纳BC V1V 1V7和加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248；

(19) Ryan R. Ransom，加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248和奥肯那根学院物理和天文系，加拿大基洛纳BC V1Y 4X8；

(20) Wolfgang Reich，马克斯·普朗克射电天文研究所，德国波恩Auf dem Hugel 69号，53121；(21) Patricia Reich，16

(22) J. Richard Shaw，不列颠哥伦比亚大学物理和天文系，加拿大温哥华BC V6T 1Z1，农业路6224号

(23) Seth R. Siegel，理论物理学边缘研究所，加拿大安大略省滑铁卢卡罗琳街北31号，N25 2YL，麦吉尔大学物理系，加拿大魁北克省蒙特利尔大学街3600号，H3A 2T8，和麦吉尔大学特罗蒂尔空间研究所，加拿大魁北克省蒙特利尔大学街3550号，H3A 2A7；

(24) Mehrnoosh Tahani，班廷和KIPAC奖学金：斯坦福大学卡维里粒子天体物理学和宇宙学研究所（KIPAC），美国加利福尼亚州斯坦福，94305；

(25) Alec J. M. Thomson，ATNF，CSIRO空间与天文，澳大利亚西澳本特利；

(26) Tristan Pinsonneault-Marotte，不列颠哥伦比亚大学物理和天文系，加拿大温哥华BC V6T 1Z1，农业路6224号；

(27) Haochen Wang，麻省理工学院卡维里天体物理和空间研究所，美国马萨诸塞州剑桥，马萨诸塞大道77号，02139和麻省理工学院物理系，美国马萨诸塞州剑桥，马萨诸塞大道77号，02139；

(28) Jennifer L. West，加拿大国家研究委员会赫兹伯格天文学和天体物理学研究中心多米尼恩射电天体物理天文台，加拿大彭蒂克顿BC V2A 6J9，邮政信箱248；

(29) Maik Wolleben，Skaha遥感有限公司，加拿大不列颠哥伦比亚省纳拉马塔杜松道3165号，V0H 1N0。

:::

:::info 本论文可在arxiv上获取，采用CC BY 4.0 DEED许可证。

:::

免责声明: 本网站转载的文章均来源于公开平台，仅供参考。这些文章不代表 MEXC 的观点或意见。所有版权归原作者所有。如果您认为任何转载文章侵犯了第三方权利，请联系 [email protected] 以便将其删除。MEXC 不对转载文章的及时性、准确性或完整性作出任何陈述或保证，并且不对基于此类内容所采取的任何行动或决定承担责任。转载材料仅供参考，不构成任何商业、金融、法律和/或税务决策的建议、认可或依据。