这就是为什么人工智能研究人员在谈论稀疏谱训练

链接表

摘要和1. 引言

1. 相关工作

2. 低秩适应

   3.1 LoRA和3.2 LoRA的局限性

   3.3 ReLoRA*

3. 稀疏谱训练

   4.1 预备知识和4.2 U、VT与Σ的梯度更新

   4.3 为什么SVD初始化很重要

   4.4 SST平衡利用与探索

   4.5 SST的内存高效实现和4.6 SST的稀疏性

4. 实验

   5.1 机器翻译

   5.2 自然语言生成

   5.3 双曲图神经网络

5. 结论和讨论

6. 更广泛的影响和参考文献

补充信息

A. 稀疏谱训练算法

B. 稀疏谱层梯度证明

C. 权重梯度分解证明

D. 增强梯度优于默认梯度的证明

E. SVD初始化零失真证明

F. 实验细节

G. 奇异值剪枝

H. 评估SST和GaLore：内存效率的互补方法

I. 消融研究

A 稀疏谱训练算法

B 稀疏谱层梯度证明

我们可以将W的微分表示为微分之和：

\ \

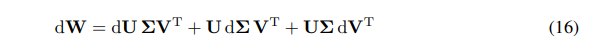
\ \ 我们有W梯度的链式法则：

\ \

\ \ \

\

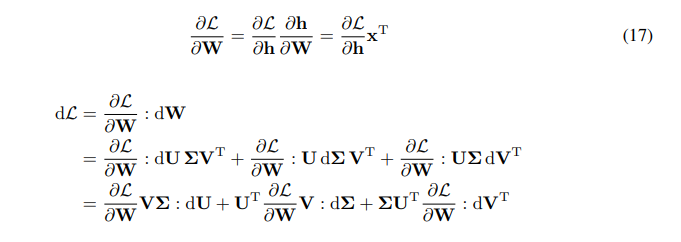
C 权重梯度分解证明

\

\

D 增强梯度优于默认梯度的证明

\

\ \ \

\ \ \

\ \ 由于只有更新方向重要，更新的规模可以通过改变学习率来调整。我们使用SST更新与全秩更新3倍之间差异的Frobenius范数来衡量相似性。

\ \

\

E SVD初始化零失真证明

\

F 实验细节

F.1 SST的实现细节

\

\ \ \

\

F.2 机器翻译的超参数

IWSLT'14。 超参数可在表6中找到。我们采用与HyboNet [12]相同的代码库和超参数，该代码库源自OpenNMT-py [54]。最终模型检查点用于评估。使用束搜索，束大小为2，以优化评估过程。实验在一台A100 GPU上进行。

\ 对于SST，每次迭代的步数(T3)设为200。每次迭代以持续20步的预热阶段开始。每轮迭代次数(T2)由公式T2 = d/r确定，其中d表示嵌入维度，r表示SST中使用的秩。

\ \

\ \ \

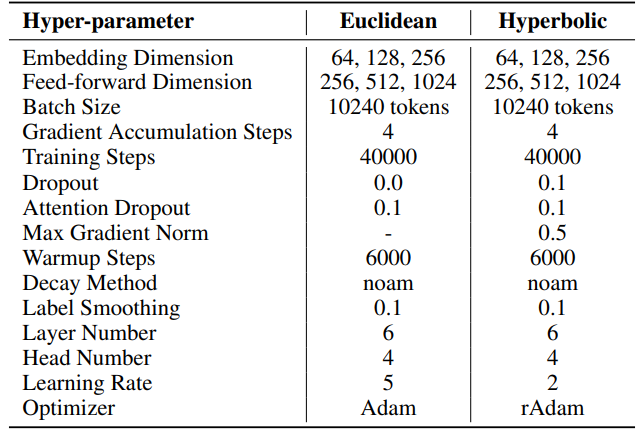
\ \ 对于SST，Multi30K的每次迭代步数(T3)设为200，IWSLT'17设为400。每次迭代以持续20步的预热阶段开始。每轮迭代次数(T2)由公式T2 = d/r确定，其中d表示嵌入维度，r表示SST中使用的秩

F.3 自然语言生成的超参数

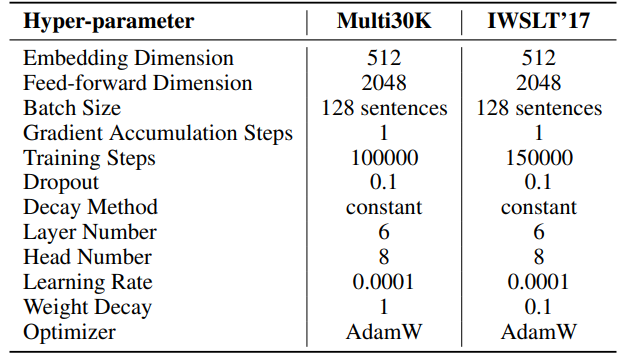
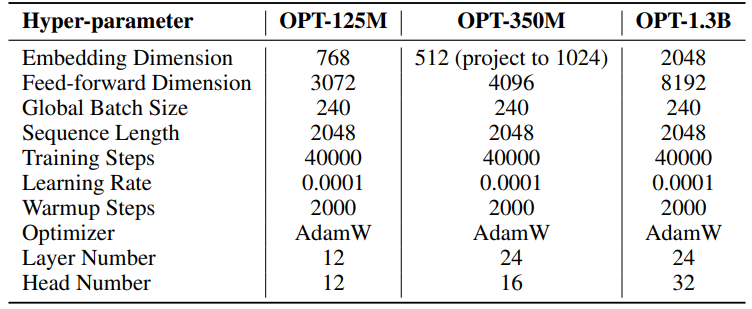
我们实验的超参数详见表8。我们采用2000步的线性预热，然后是稳定的学习率，无衰减。较大的学习率(0.001)仅用于低秩参数(SST的U、VT和Σ，LoRA和ReLoRA*的B和A)。每个实验的总训练令牌为19.7B，大约是OpenWebText的2个周期。分布式训练使用Accelerate [55]库在Linux服务器上的四个A100 GPU上进行。

\ 对于SST，每次迭代的步数(T3)设为200。每次迭代以持续20步的预热阶段开始。每轮迭代次数(T2)由公式T2 = d/r确定，其中d表示嵌入维度，r表示SST中使用的秩。

\ \

\ \ \

\

F.4 双曲图神经网络的超参数

我们使用HyboNet [12]作为全秩模型，采用与HyboNet相同的超参数。实验在一台A100 GPU上进行。

\ 对于SST，每次迭代的步数(T3)设为100。每次迭代以持续100步的预热阶段开始。每轮迭代次数(T2)由公式T2 = d/r确定，其中d表示嵌入维度，r表示SST中使用的秩。

\ 在Cora数据集上的节点分类任务中，我们为LoRA和SST方法设置了0.5的丢弃率。这是唯一一个与HyboNet配置的偏差。

\ \ \

:::info 作者：

(1) 赵佳林，复杂网络智能中心(CCNI)，清华脑与智能实验室(THBI)和计算机科学系；

(2) 张英涛，复杂网络智能中心(CCNI)，清华脑与智能实验室(THBI)和计算机科学系；

(3) 李星航，计算机科学系；

(4) 刘华平，计算机科学系；

(5) Carlo Vittorio Cannistraci，复杂网络智能中心(CCNI)，清华脑与智能实验室(THBI)，计算机科学系，以及清华大学生物医学工程系，中国北京。

:::

:::info 本论文可在arxiv上获取，采用CC by 4.0 Deed (Attribution 4.0 International)许可证。

:::

\