全息传播子：测地线和局部临界性

链接表

• 序言
• 图解规则
• 直接艾康纳尔
• 传统玻色化
• 馄饨全息
• 全息传播子
• 奇异铜酸盐
• 更奇异的事物
• 尾声

全息传播子

早期关于费米子传播子的全息研究[28]产生了许多有趣的结果，包括多重费米面（在某些极端情况下合并为一个临界"费米球"）、无色散极点以及振荡频率依赖性（后来被证明在更系统的"自上而下"构造[26]中不会出现）等。对这些结果的物理解释受到了大部分工作都是数值计算这一事实的阻碍。

\ 在mL ≫ 1的区域内可以进行简单且适合解析处理的半经典计算，其中m是推测的对偶体积费米子的质量[28, 29]。在这个区域内，费米子路径对各种量子力学振幅的贡献紧密遵循从（虚时间）作用量导出的经典边界到边界轨迹（测地线）

\

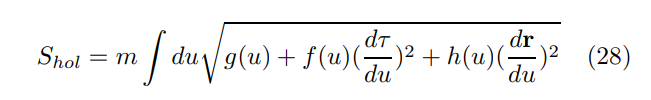
\ 通过对τ(u)和r(u)进行变分。

\ 在其测地线上评估此作用量，可得

\

\ 虽然(29)的显式解析计算只能在一些特殊情况下进行，但对于广泛的度量，可以容易地找到单参数空间/时间依赖性。具体来说，对于HV度量(26)，可得[29, 30]

\

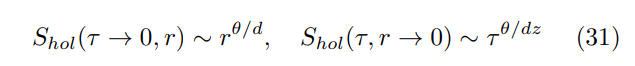
\ 值得注意的是，在没有超标度违反(θ = 0)的情况下，这两种渐近行为要么变为常数（可能性较小），要么变为对数（可能性较大，见下文）。因此，如果经典EMD拉格朗日量(22)代表边界理论与类规范相互作用(1)的有效体积对偶，则渐近行为(31)将不容易与主要依赖于z（通过η）而非θ的艾康纳尔/玻色化结果(11,21)相协调。

\

\ 并由两个独立解组成，这些解为

\

\ 施加适当的边界条件并遵循全息字典[26]，然后将传播子定义为入射在边界的波的反射系数

\

\ 当α = β + 1时，会出现不同的行为（在有限z和θ的HV度量(26)情况下无法实现），此时(33)中的积分在u → 0处发散。这种特殊的NFL区域，被称为"局部临界性"，其特征是传播子

\

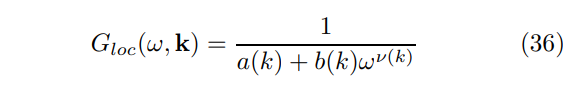
\ 其中a(k)、b(k)和ν(k) ∼ k是动量的非奇异函数，通常可以产生多个被识别为不同（"分数化"）FS[28]的极点。

\ 对(36)进行傅里叶变换的复杂性在于G(ω, k)在其参数的整个范围内并不能解析地知道。然而，通过鞍点的快速（和/或猛烈）傅里叶变换表明该函数在时空域中的形式如下

\

\ 增加了更多的复杂性，最近对2d哈伯德和t − J模型的蒙特卡洛结果表明，这些模型长期以来被认为代表铜酸盐中原型NFL正常态。这些结果并不容易符合动量独立但能量强依赖的自能函数，显示出比上述任何表达式更少的能量/温度依赖性[33]。这对由相互作用(1)支配的费米子（"自旋子"）理论在分析这些微观模型中的普遍适用性意味着什么，仍有待观察。

\

:::info 作者：

(1) D. V. Khveshchenko，北卡罗来纳大学教堂山分校物理与天文系，NC 27599。

:::

:::info 本论文可在arxiv上获取，采用CC BY 4.0 DEED许可证。

:::

\