合成高斯和树嵌入的优化性能

链接目录

摘要及 1. 引言

1. 相关工作

2. 双曲支持向量机的凸松弛技术

   3.1 预备知识

   3.2 HSVM的原始公式

   3.3 半定公式

   3.4 Moment-平方和松弛

3. 实验

   4.1 合成数据集

   4.2 真实数据集

4. 讨论、致谢及参考文献

   \

A. 证明

B. 松弛公式中的解提取

C. 关于 Moment 平方和松弛层次结构

D. Platt 缩放 [31]

E. 详细实验结果

F. 鲁棒双曲支持向量机

4.1 合成数据集

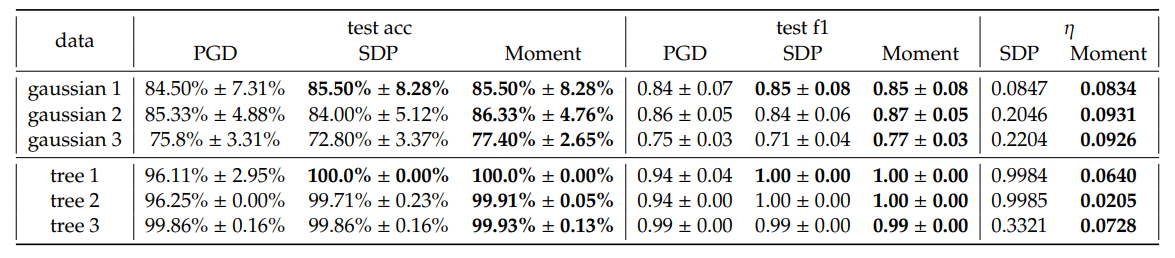
\ 总体而言，我们观察到相对于 PGD，SDP 和 Moment 在平均测试准确率和加权 F1 分数上有小幅提升。值得注意的是，我们观察到在大多数配置下，Moment 相比 SDP 通常表现出更一致的改进。此外,Moment 给出的最优性间隙 𝜂 比 SDP 更小。这符合我们的预期,即 Moment 比 SDP 更紧。

\ 尽管在某些情况下,例如当 𝐾 = 5 时,Moment 相比 PGD 和 SDP 实现了明显更小的损失,但这通常不是普遍情况。我们强调,这些损失并不是最大间隔双曲分离器泛化能力的直接测量;相反,它们是间隔最大化和错误分类惩罚的组合,后者随 𝐶 缩放。因此,观察到测试准确率和加权 F1 分数的性能更好,即使使用从 SDP 和 Moment 提取的解计算出的损失有时高于 PGD 的损失,这可能是由于复杂的损失景观造成的。更具体地说,观察到的损失增加可归因于景观的复杂性而非优化方法的有效性。根据准确率和 F1 分数结果,从经验上看,SDP 和 Moment 方法识别出的解比仅运行梯度下降获得的解具有更好的泛化能力。我们在附录 E.2 中提供了关于超参数影响的更详细分析,运行时间见表 4。高斯 1 的决策边界可视化于图 5。

\

\ 合成树嵌入。由于双曲空间适合嵌入树,我们生成随机树图并按照 Mishne 等人 [6] 将它们嵌入到 H2。具体来说,如果节点是指定节点的子节点,我们将其标记为正类,否则为负类。然后评估我们的模型进行子树分类,旨在识别一个边界,该边界包含同一子树内的所有子节点。这类任务有各种实际应用。例如,如果树代表一组标记,决策边界可以突出显示双曲空间中对应于数据图子树的语义区域。我们强调,这类子树分类任务的一个共同特征是数据不平衡,这通常导致泛化能力差。因此,我们旨在使用此任务在这个具有挑战性的设置下评估我们方法的性能。选择了三个嵌入并在图 3 中可视化,性能总结在表 1 中。所选树的运行时间可在表 4 中找到。树 2 的决策边界可视化于图 6。

\ 与合成高斯数据集的结果类似,我们观察到 SDP 和 Moment 相比 PGD 性能更好,并且由于 GD 方法通常难以应对的数据不平衡,我们在这种情况下获得了更大的加权 F1 分数提升。此外,我们观察到 SDP 的最优性间隙很大,但 Moment 的间隙非常紧,证明了即使在类别不平衡严重时 Moment 的最优性。

\

\

:::info 作者:

(1) Sheng Yang,哈佛大学 John A. Paulson 工程与应用科学学院,剑桥,麻省 ([email protected]);

(2) Peihan Liu,哈佛大学 John A. Paulson 工程与应用科学学院,剑桥,麻省 ([email protected]);

(3) Cengiz Pehlevan,哈佛大学 John A. Paulson 工程与应用科学学院,剑桥,麻省,哈佛大学脑科学中心,剑桥,麻省,以及哈佛大学自然与人工智能研究 Kempner 研究所,剑桥,麻省 ([email protected])。

:::

:::info 本论文可在 arxiv 上获取,采用 CC by-SA 4.0 Deed(署名-相同方式共享 4.0 国际)许可。

:::

\