Калибровка данных радиополяризации: улучшение корреляции между исследованиями CHIME и Dwingeloo

Таблица ссылок

Резюме и 1 Введение

1. Вращение Фарадея и Синтез Фарадея

2. Данные и инструменты

   3.1. Обзоры CHIME и GMIMS и 3.2. CHIME/GMIMS Северный низкочастотный диапазон

   3.3. Наблюдения синтезирующего телескопа DRAO

   3.4. Вспомогательные источники данных

3. Особенности Головастика

   4.1. Морфология на изображениях одной частоты

   4.2. Глубины Фарадея

   4.3. Сложность Фарадея

   4.4. QU-подгонка

   4.5. Артефакты

4. Происхождение Головастика

   5.1. Структура нейтрального водорода

   5.2. Структура ионизированного водорода

   5.3. Собственные движения звезд-кандидатов

   5.4. Глубина Фарадея и электронный столбец

5. Резюме и перспективы на будущее

\ ПРИЛОЖЕНИЕ

A. РАЗРЕШЕННЫЕ И НЕРАЗРЕШЕННЫЕ КОМПОНЕНТЫ ФАРАДЕЯ В СИНТЕЗЕ ФАРАДЕЯ

B. РЕЗУЛЬТАТЫ QU-ПОДГОНКИ

\ ССЫЛКИ

3.1. Обзоры CHIME и GMIMS

3.2. CHIME/GMIMS Северный низкочастотный диапазон

\

\ Кольцевые карты, которые мы используем, не имеют применённой деконволюции луча. В изображении есть небольшие артефакты, возникающие из-за этого, которые мы описываем в разделе 4.5, однако их присутствие не мешает изучению структур масштаба нескольких градусов, таких как головастик. В этом анализе мы используем поддиапазон 400 − 729 МГц полного диапазона CHIME, так как самые высокие частоты загрязнены наложением спектров, что делает карты ненадежными в интересующей нас области.

\ 3.2.1. Калибровка угла поляризации

\

\

\

\ Параметры Стокса U и V измеряются из продуктов перекрестной корреляции. Мы предполагаем, что ⟨V⟩ = 0 от неба в диффузном излучении, поскольку синхротронное излучение в астрофизических средах с низкой плотностью не создает круговой поляризации. Утечка между V и U возникает из-за фазовых смещений. Мы измеряем средний фазовый сдвиг ⟨ψ⟩(δ, ν) при каждом склонении и частоте, предполагая, что ⟨V⟩ = 0, и вычисляем

\

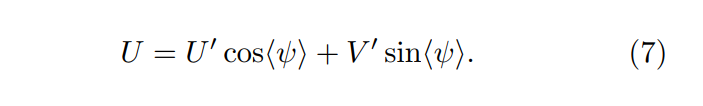
\ Предположение ⟨V⟩ = 0 приводит к высококачественным подгонкам даже в наблюдениях быстрых радиовсплесков (FRB), где это предположение имеет менее ясное физическое обоснование, чем в диффузном поляризованном излучении, которое мы исследуем (Mckinven et al. 2023). Мы обнаружили, что фазовый сдвиг линейно зависит от частоты, что согласуется с задержкой кабеля τ = ⟨ψ⟩/2πν ∼ 1 нс для диффузного излучения, как Mckinven et al. (2021, их Приложение A) обнаружили в данных CHIME/FRB.

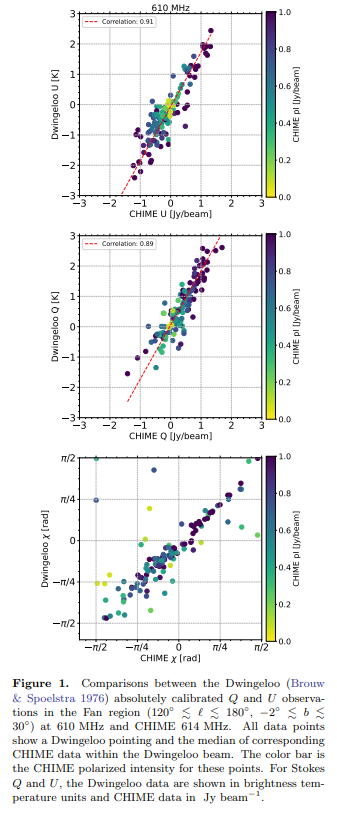
\ На рисунке 1 мы сравниваем калиброванные данные с обзором телескопа Двингелоо на частоте 610 МГц в области Веера (Brouw & Spoelstra 1976). Существует сильная корреляция между Двингелоо U и CHIME U, а также Двингелоо Q и CHIME Q в тех направлениях, для которых есть данные Двингелоо, с коэффициентами корреляции R, равными 0,91 для сравнений U − U и 0,89 для сравнений Q − Q. Это значительное улучшение по сравнению с некалиброванными коэффициентами корреляции 0,76 и 0,59 соответственно. Мы обнаружили остаточную утечку до 20% в параметре Стокса Q на основе измерений неразрешенных точечных источников. Используя среднее ортогональное расстояние между каждой точкой и подогнанной линией, мы обнаружили, что шум из данных CHIME и Двингелоо описывает ≈ 70% разброса на рисунке 1. Корреляция угла поляризации, также показанная на рисунке 1, также улучшается благодаря калибровке, и большинство выбросов — это точки с низкой поляризованной интенсивностью (желтые точки), где неопределенность в выведенном χ высока.

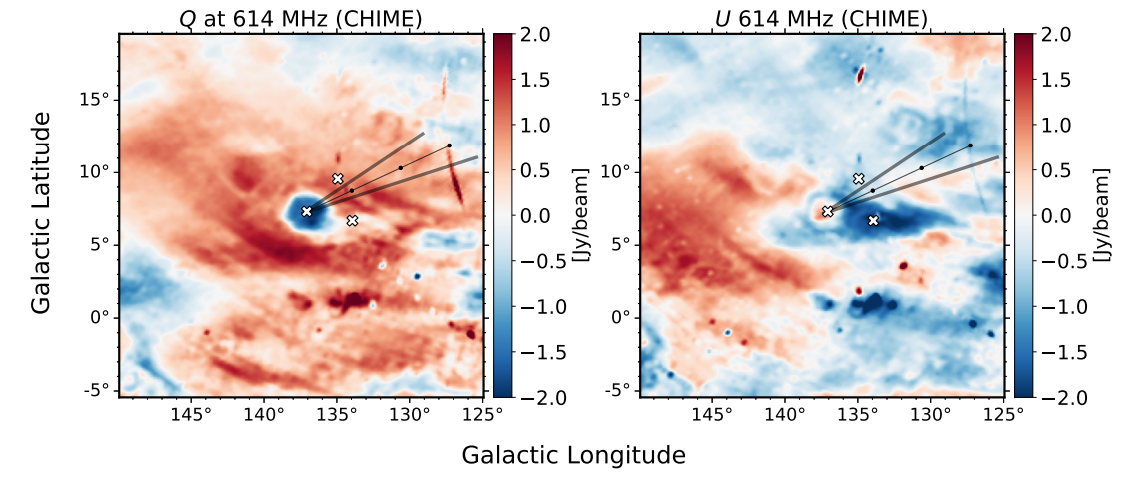
\ Мы показываем полученные карты CHIME Q и U, с опорной осью χ = 0, повернутой к северному галактическому полюсу, на рисунке 2. Хотя утечка из Стокса I в Q существует в наших данных, структура головастика не может быть просто результатом утечки. Хотя во всей области Веера, включая головастика, присутствует излучение полной интенсивности, это излучение не имеет особенностей на малых масштабах и, следовательно, не может создавать ложную поляризацию, соответствующую морфологии головастика. Кроме того, головастик не может быть продуктом излучения Стокса I, исходящего с больших угловых расстояний (например, с галактической плоскости) и наблюдаемого в дальних боковых лепестках. Хотя дальние боковые лепестки имеют плохие поляризационные свойства, их поляризация усредняется до низких значений на значительных площадях. Более того, с линейными облучателями утечка из I происходит в основном в Q, а не в U (в собственных экваториальных координатах CHIME), но головастик уже виден в Стоксе U в экваториальных координатах (не показано).

\

\

\ 3.2.2. Синтез Фарадея на данных CHIME

\

\

\ Используя алгоритм rmtools_peakfitcube в RM-Tools, мы получаем пиковую глубину Фарадея и ее

\

\ связанную ошибку для каждого спектра вдоль всех линий визирования. Полученная карта показана на рисунке 3b. Мы используем пиковые глубины Фарадея, а не первый момент (Dickey et al. 2019), чтобы сосредоточиться на глубине Фарадея самой яркой особенности в каждой линии визирования, а не на средневзвешенной глубине Фарадея в областях со сложной структурой Фарадея.

\ Мы показываем интегрированную поляризованную интенсивность по спектрам глубины Фарадея как карту нулевого момента на рисунке 3a. Карта угла поляризации, деротированная до χ0 пиковой глубиной Фарадея в каждом пикселе, показана на рисунке 3c.

\

:::info Авторы:

(1) Nasser Mohammed, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Canada and Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Canada;

(2) Anna Ordog, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okanagan Campus, Kelowna, BC V1V 1V7, Canada and Dominion Radio Astrophysical Observatory, Herzberg Research Centre for Astronomy and Astrophysics, National Research Council Canada, PO Box 248, Penticton, BC V2A 6J9, Canada;

(3) Rebecca A. Booth, Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Canada;

(4) Andrea Bracco, INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy and Laboratoire de Physique de l'Ecole Normale Superieure, ENS, Universit´e PSL, CNRS, Sorbonne Universite, Universite de Paris, F-75005 Paris, France;

(5) Jo-Anne C. Brown, Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Canada;

(6) Ettore Carretti, INAF-Istituto di Radioastronomia, Via Gobetti 101, 40129 Bologna, Italy;

(7) John M. Dickey, School of Natural Sciences, University of Tasmania, Hobart, Tas 7000 Australia;

(8) Simon Foreman, Department of Physics, Arizona State University, Tempe, AZ 85287, USA;

(9) Mark Halpern, Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T 1Z1 Canada;

(10) Marijke Haverkorn, Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands;

(11) Alex S. Hill, Department of Computer Science, Math, Physics, & Statistics, University of British Columbia, Okan