Bagaimana WormHole Mempercepat Pencarian Jalur dalam Graf dengan Miliaran Tepi

Tabel Tautan

Abstrak dan 1. Pendahuluan

1.1 Kontribusi Kami

1.2 Pengaturan

1.3 Algoritma

1. Karya Terkait

2. Algoritma

   3.1 Fase Dekomposisi Struktural

   3.2 Fase Perutean

   3.3 Varian WormHole

3. Analisis Teoretis

   4.1 Pendahuluan

   4.2 Sublinearitas Cincin Dalam

   4.3 Kesalahan Aproksimasi

   4.4 Kompleksitas Kueri

4. Hasil Eksperimental

   5.1 WormHole𝐸, WormHole𝐻 dan BiBFS

   5.2 Perbandingan dengan metode berbasis indeks

   5.3 WormHole sebagai primitif: WormHole𝑀

Referensi

1.1 Kontribusi Kami

Kami merancang algoritma baru, WormHole, yang menciptakan struktur data yang memungkinkan kami menjawab beberapa pertanyaan jalur terpendek dengan memanfaatkan struktur tipikal dari banyak jaringan sosial dan informasi. WormHole sederhana, mudah diimplementasikan, dan didukung secara teoretis. Kami menyediakan beberapa varian, masing-masing cocok untuk pengaturan yang berbeda, menunjukkan hasil empiris yang sangat baik pada berbagai dataset jaringan. Berikut adalah beberapa fitur utamanya:

\ • Pertukaran kinerja-akurasi. Sejauh pengetahuan kami, algoritma kami adalah algoritma jalur terpendek sublinear perkiraan pertama dalam jaringan besar. Fakta bahwa kami memungkinkan kesalahan aditif kecil, menimbulkan pertukaran antara waktu/ruang pra-pemrosesan dan waktu per-pertanyaan, dan memungkinkan kami untuk datang

\

\ dengan solusi dengan pra-pemrosesan yang efisien dan waktu per-pertanyaan yang cepat. Terutama, varian kami yang paling akurat (tetapi paling lambat), WormHole𝐸, memiliki akurasi hampir sempurna: lebih dari 90% pertanyaan dijawab tanpa kesalahan aditif, dan di semua jaringan, lebih dari 99% pertanyaan dijawab dengan kesalahan aditif paling banyak 2. Lihat Tabel 3 untuk detail lebih lanjut.

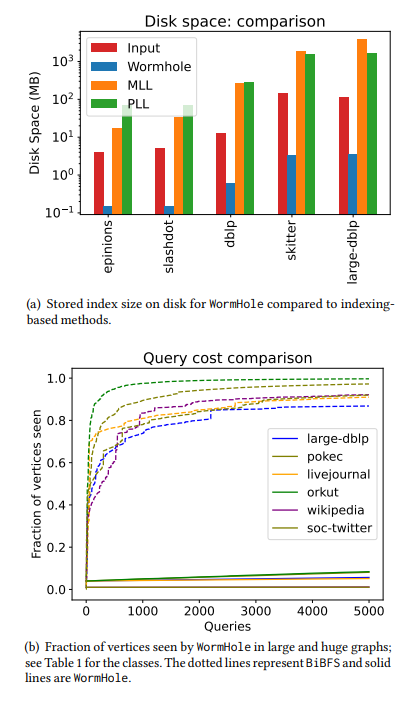
\ • Waktu pengaturan yang sangat cepat. Waktu konstruksi indeks terlama kami hanya dua menit bahkan untuk grafik dengan miliaran tepi. Untuk konteks, PLL dan MLL kehabisan waktu pada setengah dari jaringan yang kami uji, dan untuk grafik berukuran sedang di mana PLL dan MLL menyelesaikan proses mereka, konstruksi indeks WormHole ×100 lebih cepat. Yaitu, WormHole selesai dalam hitungan detik sementara PLL membutuhkan waktu berjam-jam. Lihat Tabel 4 dan Tabel 5. Waktu pengaturan yang cepat ini dicapai karena penggunaan indeks berukuran sublinear. Untuk jaringan terbesar yang kami pertimbangkan, cukup mengambil indeks sekitar 1% dari node untuk mendapatkan kesalahan aditif rata-rata kecil – lihat Tabel 1. Untuk jaringan yang lebih kecil, mungkin hingga 6%.

\ • Waktu pertanyaan yang cepat. Dibandingkan dengan BiBFS, versi vanilla WormHole𝐸 (tanpa optimasi berbasis indeks) ×2 lebih cepat untuk hampir semua grafik dan lebih dari ×4 lebih cepat pada tiga grafik terbesar yang kami uji. Varian sederhana WormHole𝐻 mencapai peningkatan satu tingkat dengan beberapa biaya akurasi: secara konsisten 20× lebih cepat di hampir semua grafik, dan lebih dari 180× untuk grafik terbesar yang kami miliki. Lihat Tabel 3 untuk perbandingan lengkap. Metode berbasis pengindeksan biasanya menjawab pertanyaan dalam mikrodetik; kedua varian yang disebutkan di atas masih dalam rezim milidetik.

\ • Menggabungkan WormHole dan teknologi terkini. WormHole bekerja dengan menyimpan subset kecil vertex di mana kami menghitung jalur terpendek yang tepat. Untuk pertanyaan sewenang-wenang, kami merutekan jalur kami melalui subset ini, yang kami sebut inti. Kami menggunakan wawasan ini untuk menyediakan varian ketiga, WormHole𝑀 dengan mengimplementasikan teknologi terkini untuk jalur terpendek, MLL, pada inti. Ini mencapai waktu pertanyaan yang sebanding dengan MLL (dengan jaminan akurasi yang sama seperti WormHole𝐻) dengan biaya pengaturan yang jauh lebih kecil, dan berjalan untuk grafik masif di mana MLL tidak berakhir. Kami mengeksplorasi pendekatan gabungan ini di §5.3, dan menyediakan statistik di Tabel 6.

\ • Kompleksitas kueri sublinear. Kompleksitas kueri mengacu pada jumlah vertex yang dikueri oleh algoritma. Dalam model akses kueri terbatas di mana mengkueri node mengungkapkan daftar tetangganya (lihat §1.2), kompleksitas kueri algoritma kami berskala sangat baik dengan jumlah pertanyaan jarak / jalur terpendek yang dibuat. Untuk menjawab 5000 pertanyaan jalur terpendek perkiraan, algoritma kami hanya mengamati antara 1% dan 20% dari node untuk sebagian besar jaringan. Sebagai perbandingan, BiBFS melihat lebih dari 90% grafik untuk menjawab beberapa ratus pertanyaan jalur terpendek. Lihat Gambar 2 dan Gambar 5 untuk perbandingan.

\ • Jaminan yang dapat dibuktikan pada kesalahan dan kinerja. Di §4 kami membuktikan serangkaian hasil teoretis yang melengkapi dan menjelaskan kinerja empiris. Hasil, yang dinyatakan secara informal di bawah ini, dibuktikan untuk model grafik acak Chung-Lu dengan distribusi derajat power-law [15–17].

\ Teorema 1.1 (Informal). Dalam grafik acak Chung-Lu 𝐺 dengan eksponen power-law 𝛽 ∈ (2,3) pada 𝑛 vertex, WormHole memiliki jaminan berikut dengan probabilitas tinggi:

\

\

:::info Penulis:

(1) Talya Eden, Universitas Bar-Ilan ([email protected]);

(2) Omri Ben-Eliezer, MIT ([email protected]);

(3) C. Seshadhri, UC Santa Cruz ([email protected]).

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC BY 4.0.

:::

\