The Mathematics of Life and Death

Table of Links

Abstract and 1. Introduction

1. The well-posed global solution

2. Nontrivial stationary solution

   3.1 Spectral theory of integro-differential operator

   3.2 The existence, uniqueness and stability of nontrivial stationary solution

3. The sharp criteria for persistence or extinction

4. The limiting behaviors of solutions with respect to advection

5. Numerical simulations

6. Discussion, Statements and Declarations, Acknowledgement, and References

3 Nontrivial stationary solution

\

3.1 Spectral theory of integro-differential operator

The eigenvalue problem is an important tool to study the longtime behaviors of elliptic and parabolic problems, especially the sign of principal eigenvalue of the linearized operator can determine the existence and stability of nontrivial stationary solution, even the persistence of species, see [20, 32, 44, 45].

\

\ And some standard properties have shown in [32].

\

\

\

\

\

3.2 The existence, uniqueness and stability of nontrivial stationary solution

Firstly, we shall the strong maximal principle for the stationary problem.

\

\

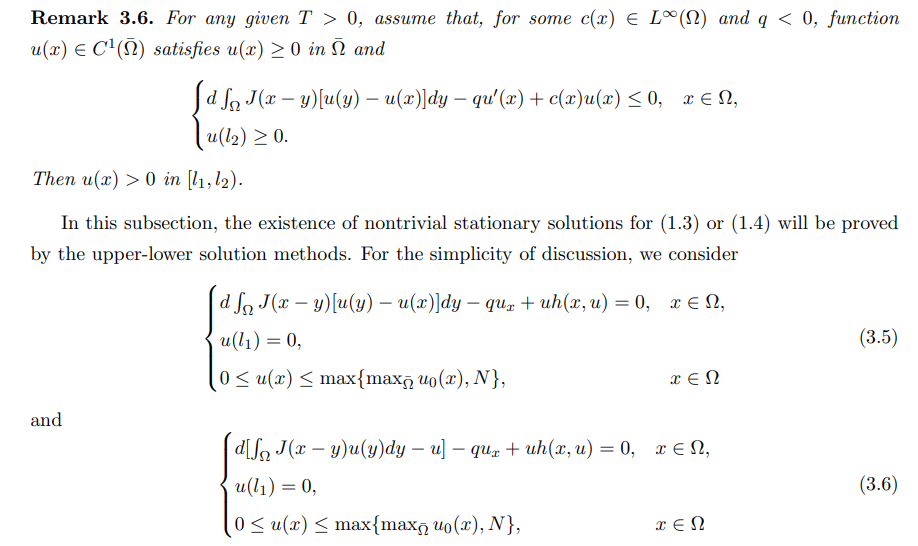
\ Notice that (3.5) (or (3.6)) has only one trivial solution u = 0.In the following, we still only consider the details for (3.5).

\

\

\

\

\

\

\

\

\

\

\

\

\

\

\

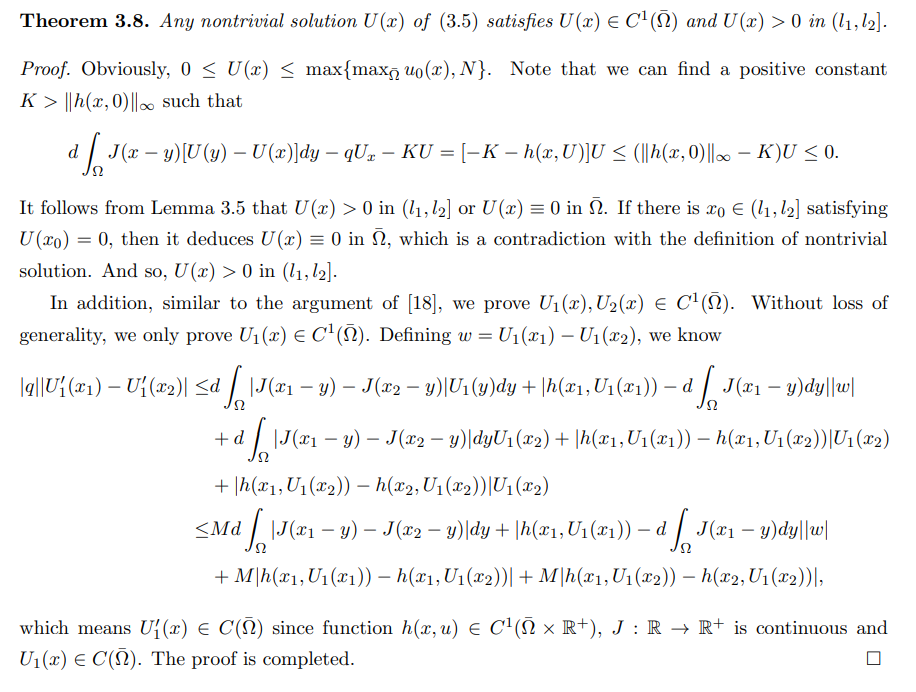
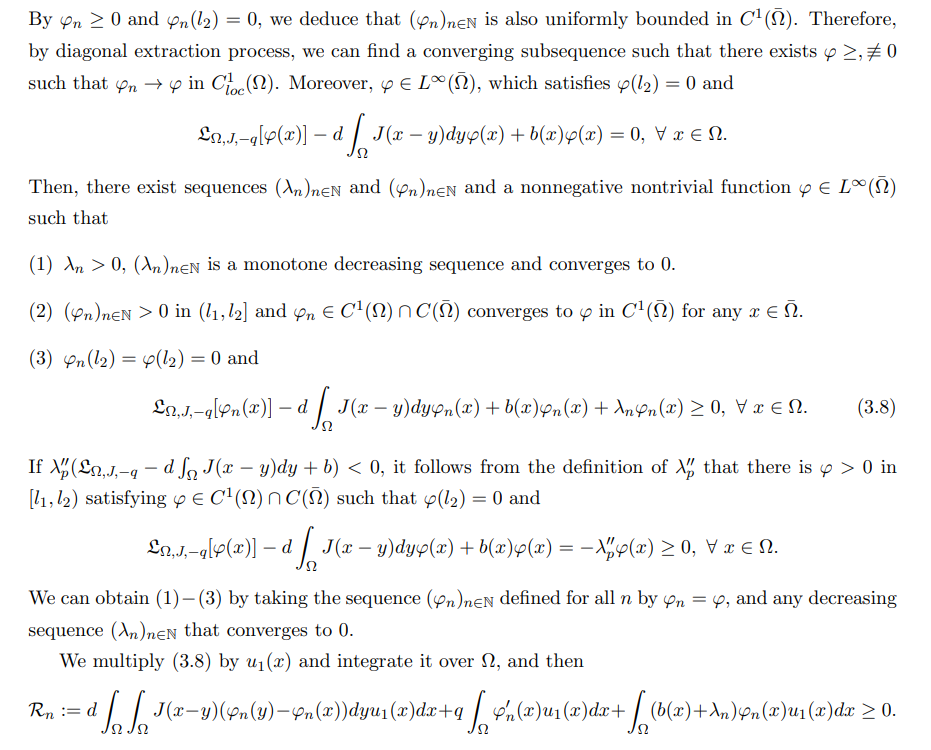
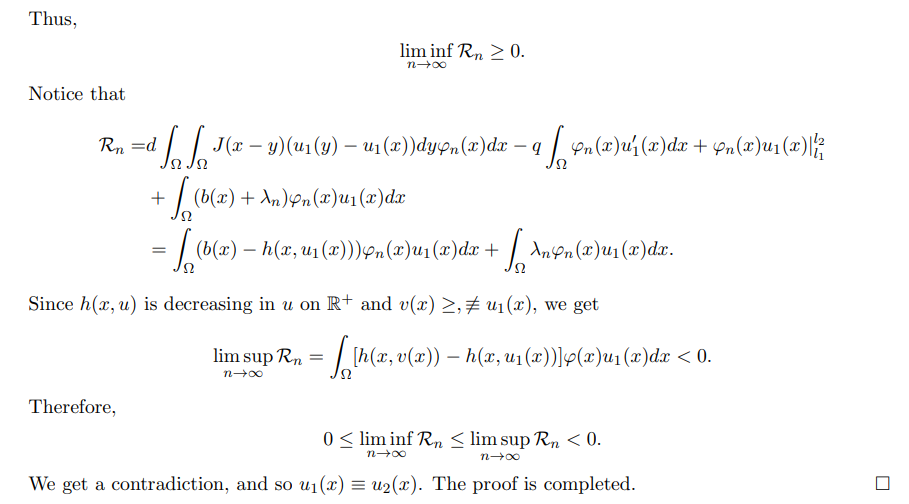
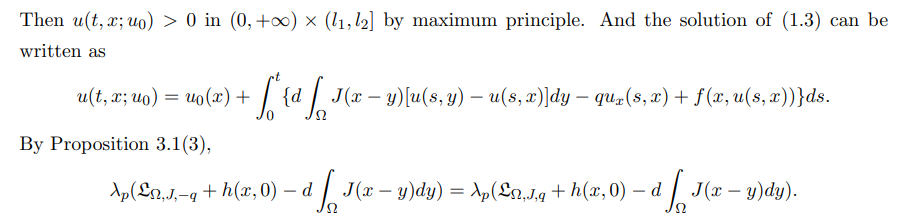
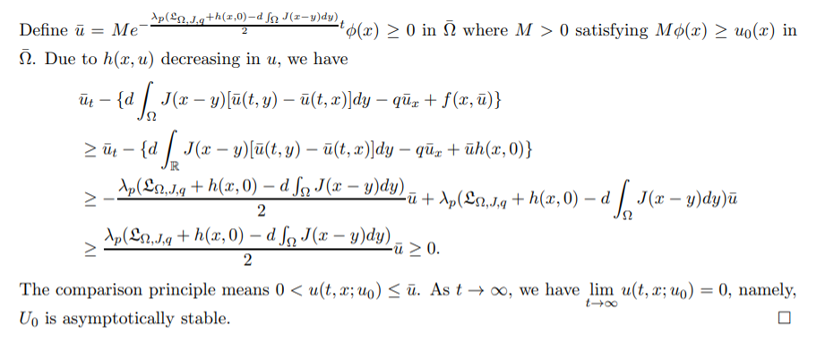
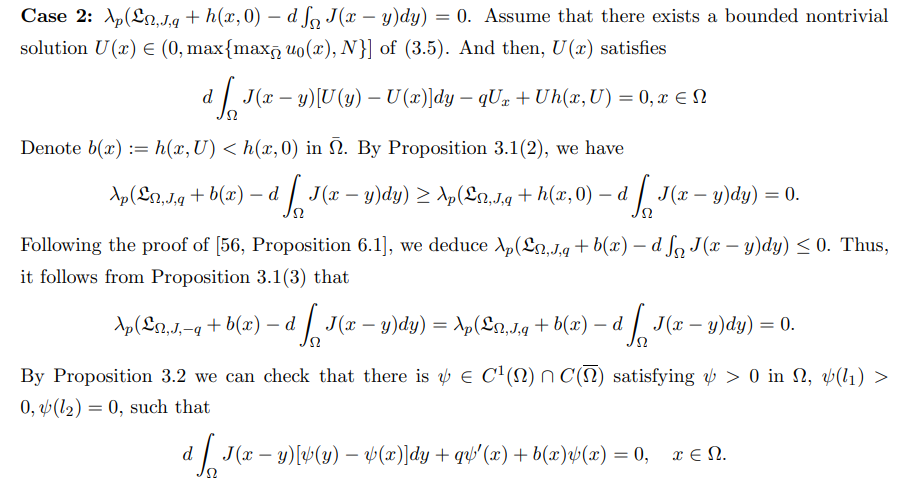
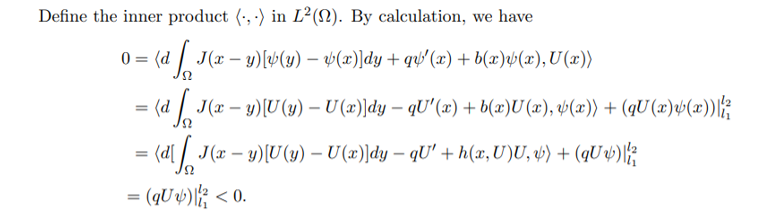
\ Hence, we obtain a contradiction, and so the theorem holds.

\

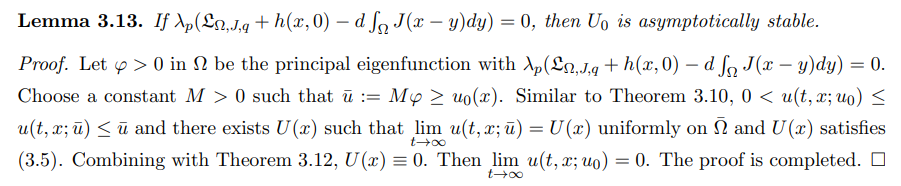
\ In summary, the results about the existence/nonexistence, uniqueness of nontrivial solutions of (3.5) and the stability of nontrivial/trivial solution are as follows.

\

\

4 The sharp criteria for persistence or extinction

\

\

\

\

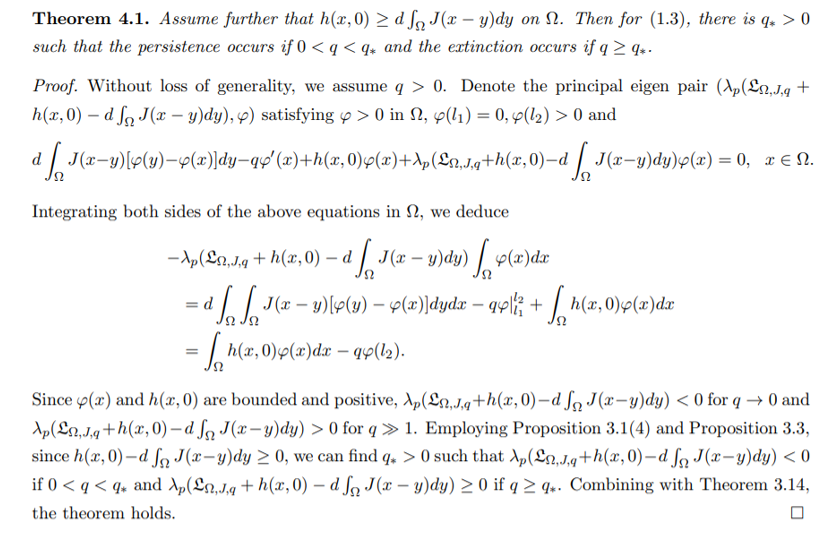
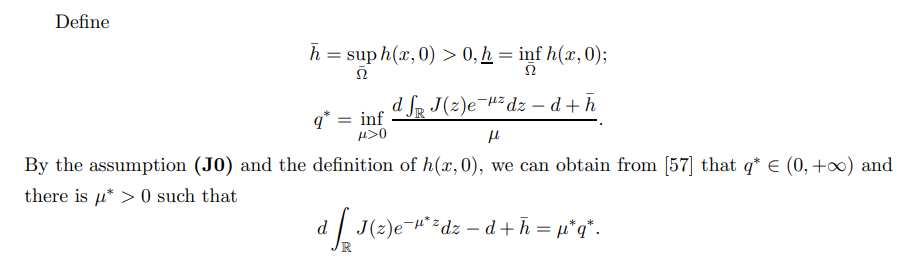
:::info Authors:

(1) Yaobin Tang, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China;

(2) Binxiang Dai, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China ([email protected]).

:::

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\