Performa Optimasi pada Embedding Gaussian dan Tree Sintetis

Daftar Tautan

Abstrak dan 1. Pendahuluan

1. Karya Terkait

2. Teknik Relaksasi Konveks untuk SVM Hiperbolik

   3.1 Pendahuluan

   3.2 Formulasi Asli HSVM

   3.3 Formulasi Semidefinit

   3.4 Relaksasi Moment-Sum-of-Squares

3. Eksperimen

   4.1 Dataset Sintetis

   4.2 Dataset Nyata

4. Diskusi, Ucapan Terima Kasih, dan Referensi

   \

A. Pembuktian

B. Ekstraksi Solusi dalam Formulasi Relaksasi

C. Tentang Hierarki Relaksasi Moment Sum-of-Squares

D. Platt Scaling [31]

E. Hasil Eksperimen Terperinci

F. Robust Hyperbolic Support Vector Machine

4.1 Dataset Sintetis

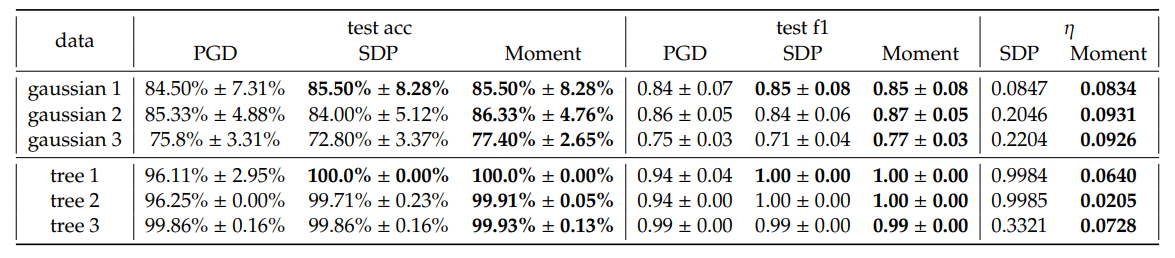
\ Secara umum, kami mengamati peningkatan kecil dalam akurasi pengujian rata-rata dan skor F1 tertimbang dari SDP dan Moment relatif terhadap PGD. Khususnya, kami mengamati bahwa Moment sering menunjukkan peningkatan yang lebih konsisten dibandingkan dengan SDP, di sebagian besar konfigurasi. Selain itu, Moment memberikan kesenjangan optimalitas 𝜂 yang lebih kecil daripada SDP. Ini sesuai dengan ekspektasi kami bahwa Moment lebih ketat daripada SDP.

\ Meskipun dalam beberapa kasus, misalnya ketika 𝐾 = 5, Moment mencapai kerugian yang jauh lebih kecil dibandingkan dengan PGD dan SDP, ini umumnya bukan kasusnya. Kami menekankan bahwa kerugian ini bukan pengukuran langsung dari kemampuan generalisasi pemisah hiperbolik margin-maksimum; melainkan, mereka adalah kombinasi dari maksimalisasi margin dan penalti untuk kesalahan klasifikasi yang berskala dengan 𝐶. Oleh karena itu, pengamatan bahwa kinerja dalam akurasi pengujian dan skor F1 tertimbang lebih baik, meskipun kerugian yang dihitung menggunakan solusi yang diekstraksi dari SDP dan Moment kadang-kadang lebih tinggi daripada dari PGD, mungkin disebabkan oleh lanskap kerugian yang rumit. Lebih khusus lagi, peningkatan kerugian yang diamati dapat dikaitkan dengan kerumitan lanskap daripada efektivitas metode optimasi. Berdasarkan hasil akurasi dan skor F1, secara empiris metode SDP dan Moment mengidentifikasi solusi yang menggeneralisasi lebih baik daripada yang diperoleh dengan menjalankan gradient descent saja. Kami memberikan analisis yang lebih rinci tentang efek hiperparameter di Lampiran E.2 dan waktu eksekusi di Tabel 4. Batas keputusan untuk Gaussian 1 divisualisasikan dalam Gambar 5.

\

\ Synthetic Tree Embedding. Karena ruang hiperbolik baik untuk embedding pohon, kami menghasilkan grafik pohon acak dan menanamkannya ke H2 mengikuti Mishne et al. [6]. Secara khusus, kami memberi label node sebagai positif jika mereka adalah anak dari node yang ditentukan dan negatif sebaliknya. Model kami kemudian dievaluasi untuk klasifikasi subpohon, yang bertujuan untuk mengidentifikasi batas yang mencakup semua node anak dalam subpohon yang sama. Tugas seperti itu memiliki berbagai aplikasi praktis. Misalnya, jika pohon mewakili satu set token, batas keputusan dapat menyoroti wilayah semantik di ruang hiperbolik yang sesuai dengan subpohon dari grafik data. Kami menekankan bahwa fitur umum dalam tugas klasifikasi subpohon tersebut adalah ketidakseimbangan data, yang biasanya menyebabkan kemampuan generalisasi yang buruk. Oleh karena itu, kami bertujuan menggunakan tugas ini untuk menilai kinerja metode kami dalam pengaturan yang menantang ini. Tiga embedding dipilih dan divisualisasikan dalam Gambar 3 dan kinerjanya dirangkum dalam Tabel 1. Waktu eksekusi pohon yang dipilih dapat ditemukan di Tabel 4. Batas keputusan pohon 2 divisualisasikan dalam Gambar 6.

\ Mirip dengan hasil dataset Gaussian sintetis, kami mengamati kinerja yang lebih baik dari SDP dan Moment dibandingkan dengan PGD, dan karena ketidakseimbangan data yang biasanya menjadi kesulitan metode GD, kami memiliki peningkatan yang lebih besar dalam skor F1 tertimbang dalam kasus ini. Selain itu, kami mengamati kesenjangan optimalitas yang besar untuk SDP tetapi kesenjangan yang sangat ketat untuk Moment, membuktikan optimalitas Moment bahkan ketika ketidakseimbangan kelas parah.

\

\

:::info Penulis:

(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);

(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);

(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, dan Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA ([email protected]).

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International).

:::

\