Inilah Mengapa Peneliti AI Membicarakan Sparse Spectral Training

Tabel Tautan

Abstrak dan 1. Pendahuluan

1. Karya Terkait

2. Adaptasi Peringkat Rendah

   3.1 LoRA dan 3.2 Keterbatasan LoRA

   3.3 ReLoRA*

3. Pelatihan Spektral Jarang

   4.1 Pendahuluan dan 4.2 Pembaruan Gradien U, VT dengan Σ

   4.3 Mengapa Inisialisasi SVD Penting

   4.4 SST Menyeimbangkan Eksploitasi dan Eksplorasi

   4.5 Implementasi Hemat Memori untuk SST dan 4.6 Kejarangan SST

4. Eksperimen

   5.1 Terjemahan Mesin

   5.2 Generasi Bahasa Alami

   5.3 Jaringan Saraf Graf Hiperbolik

5. Kesimpulan dan Diskusi

6. Dampak Lebih Luas dan Referensi

Informasi Tambahan

A. Algoritma Pelatihan Spektral Jarang

B. Bukti Gradien Lapisan Spektral Jarang

C. Bukti Dekomposisi Gradien Bobot

D. Bukti Keunggulan Gradien yang Ditingkatkan dibandingkan Gradien Default

E. Bukti Distorsi Nol dengan Inisialisasi SVD

F. Detail Eksperimen

G. Pemangkasan Nilai Singular

H. Mengevaluasi SST dan GaLore: Pendekatan Komplementer untuk Efisiensi Memori

I. Studi Ablasi

A Algoritma Pelatihan Spektral Jarang

B Bukti Gradien Lapisan Spektral Jarang

Kita dapat mengekspresikan diferensial dari W sebagai jumlah diferensial:

\ \

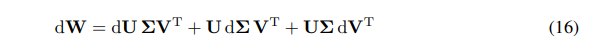
\ \ Kita memiliki aturan rantai untuk gradien W:

\ \

\ \ \

\

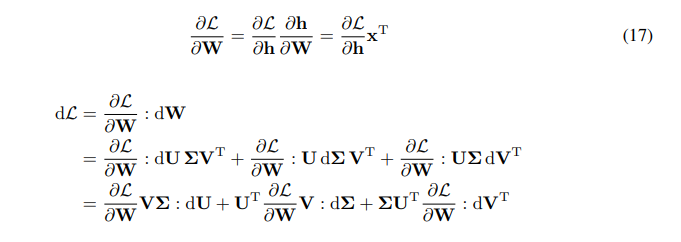
C Bukti Dekomposisi Gradien Bobot

\

\

D Bukti Keunggulan Gradien yang Ditingkatkan dibandingkan Gradien Default

\

\ \ \

\ \ \

\ \ Karena hanya arah pembaruan yang penting, skala pembaruan dapat disesuaikan dengan mengubah tingkat pembelajaran. Kami mengukur kemiripan menggunakan norma Frobenius dari perbedaan antara pembaruan SST dan 3 kali pembaruan peringkat penuh.

\ \

\

E Bukti Distorsi Nol dengan Inisialisasi SVD

\

F Detail Eksperimen

F.1 Detail Implementasi untuk SST

\

\ \ \

\

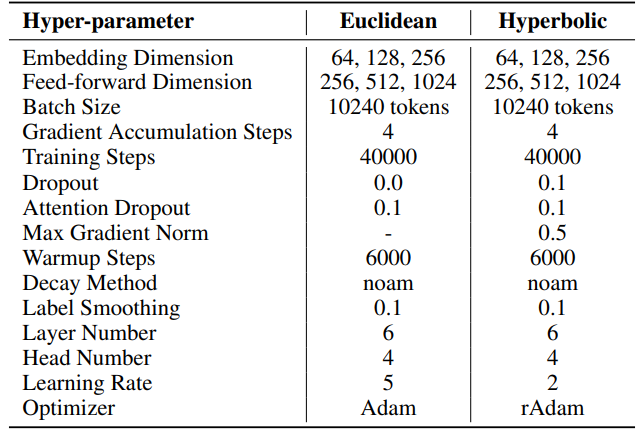
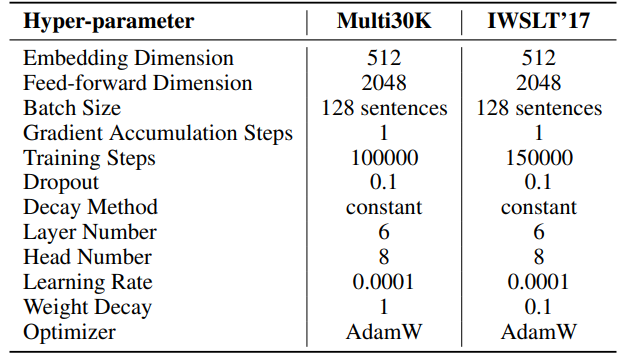
F.2 Hiperparameter Terjemahan Mesin

IWSLT'14. Hiperparameter dapat ditemukan di Tabel 6. Kami menggunakan basis kode dan hiperparameter yang sama seperti yang digunakan dalam HyboNet [12], yang berasal dari OpenNMT-py [54]. Model checkpoint terakhir digunakan untuk evaluasi. Pencarian beam, dengan ukuran beam 2, digunakan untuk mengoptimalkan proses evaluasi. Eksperimen dilakukan pada satu GPU A100.

\ Untuk SST, jumlah langkah per iterasi (T3) ditetapkan menjadi 200. Setiap iterasi dimulai dengan fase pemanasan yang berlangsung 20 langkah. Jumlah iterasi per putaran (T2) ditentukan oleh rumus T2 = d/r, di mana d mewakili dimensi embedding dan r menunjukkan peringkat yang digunakan dalam SST.

\ \

\ \ \

\ \ Untuk SST, jumlah langkah per iterasi (T3) ditetapkan menjadi 200 untuk Multi30K dan 400 untuk IWSLT'17. Setiap iterasi dimulai dengan fase pemanasan yang berlangsung 20 langkah. Jumlah iterasi per putaran (T2) ditentukan oleh rumus T2 = d/r, di mana d mewakili dimensi embedding dan r menunjukkan peringkat yang digunakan dalam SST

F.3 Hiperparameter Generasi Bahasa Alami

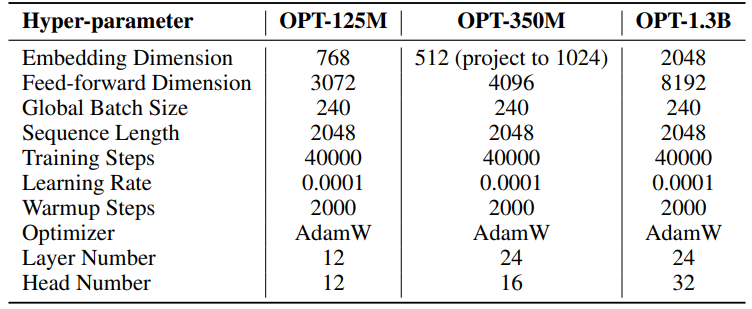
Hiperparameter untuk eksperimen kami dijelaskan secara rinci dalam Tabel 8. Kami menggunakan pemanasan linear 2000 langkah diikuti dengan tingkat pembelajaran yang stabil, tanpa penurunan. Tingkat pembelajaran yang lebih besar (0,001) digunakan hanya untuk parameter peringkat rendah (U, VT dan Σ untuk SST, B dan A untuk LoRA dan ReLoRA*. Total token pelatihan untuk setiap eksperimen adalah 19,7B, sekitar 2 epoch OpenWebText. Pelatihan terdistribusi difasilitasi menggunakan pustaka Accelerate [55] di empat GPU A100 pada server Linux.

\ Untuk SST, jumlah langkah per iterasi (T3) ditetapkan menjadi 200. Setiap iterasi dimulai dengan fase pemanasan yang berlangsung 20 langkah. Jumlah iterasi per putaran (T2) ditentukan oleh rumus T2 = d/r, di mana d mewakili dimensi embedding dan r menunjukkan peringkat yang digunakan dalam SST.

\ \

\ \ \

\

F.4 Hiperparameter Jaringan Saraf Graf Hiperbolik

Kami menggunakan HyboNet [12] sebagai model peringkat penuh, dengan hiperparameter yang sama seperti yang digunakan dalam HyboNet. Eksperimen dilakukan pada satu GPU A100.

\ Untuk SST, jumlah langkah per iterasi (T3) ditetapkan menjadi 100. Setiap iterasi dimulai dengan fase pemanasan yang berlangsung 100 langkah. Jumlah iterasi per putaran (T2) ditentukan oleh rumus T2 = d/r, di mana d mewakili dimensi embedding dan r menunjukkan peringkat yang digunakan dalam SST.

\ Kami menetapkan tingkat dropout menjadi 0,5 untuk metode LoRA dan SST selama tugas klasifikasi node pada dataset Cora. Ini adalah satu-satunya penyimpangan dari konfigurasi HyboNet.

\ \ \

:::info Penulis:

(1) Jialin Zhao, Pusat Kecerdasan Jaringan Kompleks (CCNI), Laboratorium Otak dan Kecerdasan Tsinghua (THBI) dan Departemen Ilmu Komputer;

(2) Yingtao Zhang, Pusat Kecerdasan Jaringan Kompleks (CCNI), Laboratorium Otak dan Kecerdasan Tsinghua (THBI) dan Departemen Ilmu Komputer;

(3) Xinghang Li, Departemen Ilmu Komputer;

(4) Huaping Liu, Departemen Ilmu Komputer;

(5) Carlo Vittorio Cannistraci, Pusat Kecerdasan Jaringan Kompleks (CCNI), Laboratorium Otak dan Kecerdasan Tsinghua (THBI), Departemen Ilmu Komputer, dan Departemen Teknik Biomedis Universitas Tsinghua, Beijing, Tiongkok.

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC by 4.0 Deed (Atribusi 4.0 Internasional).

:::

\