How Mixture-of-Adaptations Makes Language Model Fine-Tuning Cheaper and Smarter

Table of Links

Abstract and 1. Introduction

1. Background

   2.1 Mixture-of-Experts

   2.2 Adapters

2. Mixture-of-Adaptations

   3.1 Routing Policy

   3.2 Consistency regularization

   3.3 Adaptation module merging and 3.4 Adaptation module sharing

   3.5 Connection to Bayesian Neural Networks and Model Ensembling

3. Experiments

   4.1 Experimental Setup

   4.2 Key Results

   4.3 Ablation Study

4. Related Work

5. Conclusions

6. Limitations

7. Acknowledgment and References

Appendix

A. Few-shot NLU Datasets B. Ablation Study C. Detailed Results on NLU Tasks D. Hyper-parameter

3 Mixture-of-Adaptations

\

3.1 Routing Policy

Recent work like THOR (Zuo et al., 2021) has demonstrated stochastic routing policy like random routing to work as well as classical routing mechanism like Switch routing (Fedus et al., 2021) with the following benefits. Since input examples are randomly routed to different experts, there is no requirement for additional load balancing as each expert has an equal opportunity of being activated simplifying the framework. Further, there are no added parameters, and therefore no additional computation, at the Switch layer for expert selection. The latter is particularly important in our setting for parameter-efficient fine-tuning to keep the parameters and FLOPs the same as that of a single adaptation module. To analyze the working of AdaMix, we demonstrate connections to stochastic routing and model weight averaging to Bayesian Neural Networks and model ensembling in Section 3.5.

\ \

\ \ Such stochastic routing enables adaptation modules to learn different transformations during training and obtain multiple views of the task. However, this also creates a challenge on which modules to use during inference due to random routing protocol during training. We address this challenge with the following two techniques that further allow us to collapse adaptation modules and obtain the same computational cost (FLOPs, #tunable adaptation parameters) as that of a single module.

3.2 Consistency regularization

\

\ \ \

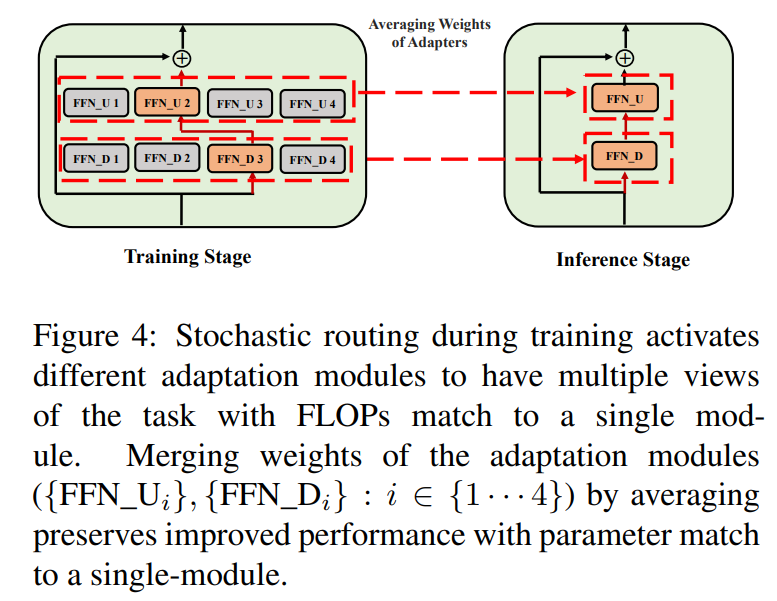
3.3 Adaptation module merging

While the above regularization mitigates inconsistency in random module selection during inference, it still results in increased serving cost to host several adaptation modules. Prior works in fine-tuning language models for downstream tasks have shown improved performance on averaging the weights of different models fine-tuned with different random seeds outperforming a single fine-tuned model. Recent work (Wortsman et al., 2022) has also shown that differently fine-tuned models from the same initialization lie in the same error basin motivating the use of weight aggregation for robust task summarization. We adopt and extend prior techniques for language model fine-tuning to our parameterefficient training of multi-view adaptation modules

\ \

\

3.4 Adaptation module sharing

\

3.5 Connection to Bayesian Neural Networks and Model Ensemblin

\

\ \ This requires averaging over all possible model weights, which is intractable in practice. Therefore, several approximation methods have been developed based on variational inference methods and stochastic regularization techniques using dropouts. In this work, we leverage another stochastic regularization in the form of random routing. Here, the objective is to find a surrogate distribution qθ(w) in a tractable family of distributions that can replace the true model posterior that is hard to compute. The ideal surrogate is identified by minimizing the Kullback-Leibler (KL) divergence between the candidate and the true posterior.

\ \

\ \ \

\ \ \

\ \ \ \

:::info Authors:

(1) Yaqing Wang, Purdue University ([email protected]);

(2) Sahaj Agarwal, Microsoft ([email protected]);

(3) Subhabrata Mukherjee, Microsoft Research ([email protected]);

(4) Xiaodong Liu, Microsoft Research ([email protected]);

(5) Jing Gao, Purdue University ([email protected]);

(6) Ahmed Hassan Awadallah, Microsoft Research ([email protected]);

(7) Jianfeng Gao, Microsoft Research ([email protected]).

:::

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\