Bagaimana Toto Membayangkan Kembali Multi-Head Attention untuk Peramalan Multivariat

Tabel Tautan

1. Latar belakang
2. Pernyataan masalah
3. Arsitektur model
4. Data pelatihan
5. Hasil
6. Kesimpulan
7. Pernyataan dampak
8. Arah masa depan
9. Kontribusi
10. Ucapan terima kasih dan Referensi

Lampiran

3 Arsitektur model

Toto adalah model peramalan decoder-only. Model ini menggunakan banyak teknik terbaru dari literatur, dan memperkenalkan metode baru untuk mengadaptasi perhatian multi-head ke data deret waktu multivariat (Gbr. 1).

\ 3.1 Desain Transformer

\ Model Transformer untuk peramalan deret waktu telah menggunakan berbagai arsitektur encoder-decoder [12, 13, 21], encoder-only [14, 15, 17], dan decoder-only [19, 23]. Untuk Toto, kami menggunakan arsitektur decoder-only. Arsitektur decoder telah terbukti dapat diskalakan dengan baik [25, 26], dan memungkinkan cakrawala prediksi yang arbitrer. Tugas prediksi patch berikutnya yang bersifat kausal juga menyederhanakan proses pra-pelatihan.

\ Kami menggunakan teknik dari beberapa arsitektur model bahasa besar (LLM) terbaru, termasuk prenormalisasi [27], RMSNorm [28], dan lapisan feed-forward SwiGLU [29].

\ 3.2 Embedding input

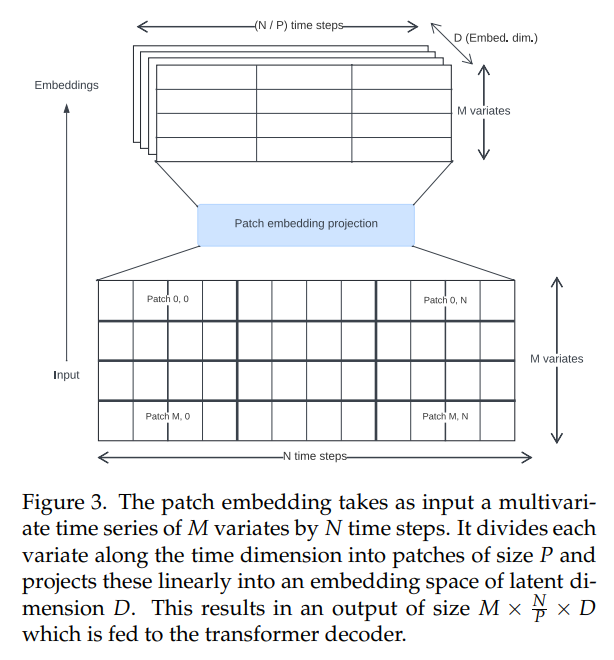
\ Transformer deret waktu dalam literatur telah menggunakan berbagai pendekatan untuk membuat embedding input. Kami menggunakan proyeksi patch yang tidak tumpang tindih (Gbr. 3), yang pertama kali diperkenalkan untuk Vision Transformers [30, 31] dan dipopulerkan dalam konteks deret waktu oleh PatchTST [14]. Toto dilatih menggunakan ukuran patch tetap sebesar 32.

\

\ 3.3 Mekanisme perhatian

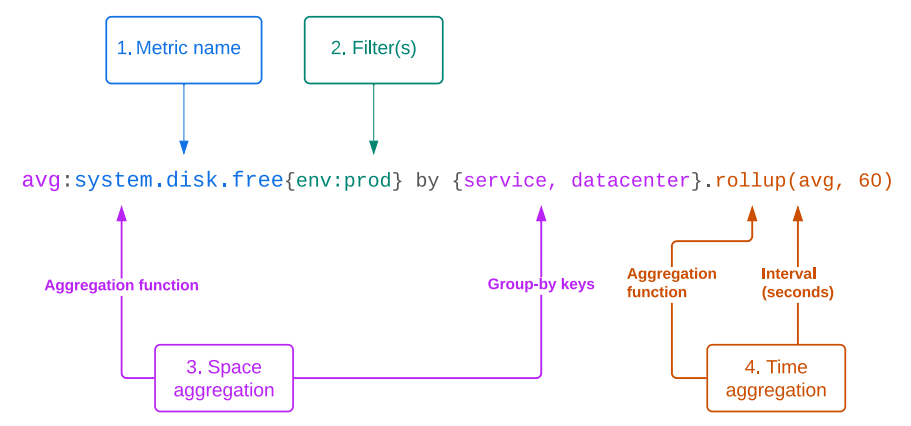
\ Metrik observabilitas sering kali merupakan deret waktu multivariat dengan kardinalitas tinggi. Oleh karena itu, model yang ideal akan secara alami menangani peramalan multivariat. Model tersebut harus dapat menganalisis hubungan baik dalam dimensi waktu (yang kami sebut sebagai interaksi "time-wise") dan dalam dimensi saluran (yang kami sebut sebagai interaksi "space-wise", mengikuti konvensi dalam platform Datadog yang menggambarkan kelompok atau set tag yang berbeda dari metrik sebagai dimensi "space").

\ Untuk memodelkan interaksi space dan time-wise, kita perlu mengadaptasi arsitektur perhatian multi-head tradisional [11] dari satu ke dua dimensi. Beberapa pendekatan telah diusulkan dalam literatur untuk melakukan ini, termasuk:

\ • Mengasumsikan independensi saluran, dan menghitung perhatian hanya dalam dimensi waktu [14]. Ini efisien, tetapi membuang semua informasi tentang interaksi space-wise.

\ • Menghitung perhatian hanya dalam dimensi ruang, dan menggunakan jaringan feed-forward dalam dimensi waktu [17, 18].

\ • Menggabungkan variat sepanjang dimensi waktu dan menghitung perhatian silang penuh antara setiap lokasi ruang/waktu [15]. Ini dapat menangkap setiap interaksi ruang dan waktu yang mungkin, tetapi secara komputasi mahal.

\ • Menghitung "perhatian terfaktorisasi," di mana setiap blok transformer berisi perhitungan perhatian ruang dan waktu yang terpisah [16, 32, 33]. Ini memungkinkan pencampuran ruang dan waktu, dan lebih efisien daripada perhatian silang penuh. Namun, ini menggandakan kedalaman efektif jaringan.

\ Untuk merancang mekanisme perhatian kami, kami mengikuti intuisi bahwa untuk banyak deret waktu, hubungan waktu lebih penting atau prediktif daripada hubungan ruang. Sebagai bukti, kami mengamati bahwa bahkan model yang sepenuhnya mengabaikan hubungan space-wise (seperti PatchTST [14] dan TimesFM [19]) masih dapat mencapai kinerja yang kompetitif pada dataset multivariat. Namun, studi lain (misalnya Moirai [15]) telah menunjukkan melalui ablasi bahwa ada beberapa manfaat yang jelas dengan memasukkan hubungan space-wise.

\ Oleh karena itu, kami mengusulkan varian baru dari perhatian terfaktorisasi, yang kami sebut "Perhatian Ruang-Waktu Terfaktorisasi Proporsional." Kami menggunakan campuran blok perhatian space-wise dan time-wise yang bergantian. Sebagai hiperparameter yang dapat dikonfigurasi, kita dapat mengubah rasio blok time-wise terhadap space-wise, sehingga memungkinkan kita untuk mengalokasikan lebih banyak atau lebih sedikit anggaran komputasi untuk setiap jenis perhatian. Untuk model dasar kami, kami memilih konfigurasi dengan satu blok perhatian space-wise untuk setiap dua blok time-wise.

\ Dalam blok perhatian time-wise, kami menggunakan masking kausal dan embedding posisional rotary [34] dengan XPOS [35] untuk memodelkan fitur yang bergantung pada waktu secara autoregresif. Dalam blok space-wise, sebaliknya, kami menggunakan perhatian bidireksional penuh untuk mempertahankan invariansi permutasi dari kovariat, dengan mask ID blok-diagonal untuk memastikan bahwa hanya variat terkait yang memperhatikan satu sama lain. Masking ini memungkinkan kami untuk mengemas beberapa deret waktu multivariat independen ke dalam batch yang sama, untuk meningkatkan efisiensi pelatihan dan mengurangi jumlah padding.

\ 3.4 Kepala prediksi probabilistik

\ Agar berguna untuk aplikasi peramalan, model harus menghasilkan prediksi probabilistik. Praktik umum dalam model deret waktu adalah menggunakan lapisan output di mana model meregresikan parameter distribusi probabilitas. Ini memungkinkan interval prediksi dihitung menggunakan sampling Monte Carlo [7].

\ Pilihan umum untuk lapisan output adalah Normal [7] dan Student-T [23, 36], yang dapat meningkatkan ketahanan terhadap outlier. Moirai [15] memungkinkan distribusi residual yang lebih fleksibel dengan mengusulkan model campuran baru yang menggabungkan kombinasi tertimbang dari output Gaussian, Student-T, Log-Normal, dan Negative-Binomial.

\ Namun, deret waktu dunia nyata sering memiliki distribusi kompleks yang sulit untuk disesuaikan, dengan outlier, ekor berat, kemiringan ekstrem, dan multimodalitas. Untuk mengakomodasi skenario ini, kami memperkenalkan kemungkinan output yang lebih fleksibel. Untuk melakukan ini, kami menggunakan metode berdasarkan model campuran Gaussian (GMMs), yang dapat memperkirakan fungsi kepadatan apa pun ([37]). Untuk menghindari ketidakstabilan pelatihan dengan adanya outlier, kami menggunakan model campuran Student-T (SMM), generalisasi GMMs yang kuat [38] yang sebelumnya telah menunjukkan harapan untuk pemodelan deret waktu keuangan berekor berat [39, 40]. Model memprediksi k distribusi Student-T (di mana k adalah hiperparameter) untuk setiap langkah waktu, serta pembobotan yang dipelajari.

\

\ Ketika kami melakukan inferensi, kami mengambil sampel dari distribusi campuran pada setiap timestamp, kemudian memasukkan kembali setiap sampel ke dalam decoder untuk prediksi berikutnya. Ini memungkinkan kami untuk menghasilkan interval prediksi pada kuantil mana pun, dibatasi hanya oleh jumlah sampel; untuk ekor yang lebih presisi, kita dapat memilih untuk menghabiskan lebih banyak komputasi pada sampling (Gbr. 2).

\ 3.5 Penskalaan input/output

\ Seperti dalam model deret waktu lainnya, kami melakukan normalisasi instance pada data input sebelum meneruskannya melalui embedding patch, untuk membuat model menggeneralisasi lebih baik ke input dengan skala yang berbeda [41]. Kami menskalakan input agar memiliki rata-rata nol dan deviasi standar unit. Prediksi output kemudian diskalakan kembali ke unit asli.

\ 3.6 Tujuan pelatihan

\ Sebagai model decoder-only, Toto dilatih sebelumnya pada tugas prediksi patch berikutnya. Kami meminimalkan negative log-likelihood dari patch yang diprediksi berikutnya sehubungan dengan output distribusi model. Kami melatih model menggunakan optimizer AdamW [42].

\ 3.7 Hiperparameter

\ Hiperparameter yang digunakan untuk Toto dijelaskan secara rinci dalam Tabel A.1, dengan total 103 juta parameter.

\

:::info Penulis:

(1) Ben Cohen ([email protected]);

(2) Emaad Khwaja ([email protected]);

(3) Kan Wang ([email protected]);

(4) Charles Masson ([email protected]);

(5) Elise Rame ([email protected]);

(6) Youssef Doubli ([email protected]);

(7) Othmane Abou-Amal ([email protected]).

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC BY 4.0.

:::

\