Tidak Ada Pemenang di Sini: Mengapa Setiap Lelang Kripto yang "Adil" Berakhir Sepele

Tabel Tautan

Abstrak dan 1. Pendahuluan

1.1 Ikhtisar Teknis

1.2 Karya Terkait

1. Model dan Pendahuluan dan 2.1 Mekanisme Biaya Transaksi

   2.2 Desiderata TFM

2. Memahami OCA

   3.1 Perbedaan Antara SCP dan OCA

   3.2 Hasil Pendahuluan yang Berguna untuk TFM yang OCA-proof

3. Mekanisme Deterministik OCA-proof

4. Mekanisme Teracak OCA-proof

5. Diskusi dan Referensi

   \

A. Bukti yang Hilang

B. Mekanisme Deterministik Non-anonim

4 Mekanisme Deterministik OCA-proof

Contoh 3.6 menunjukkan bahwa secara umum, properti DSIC dan 1-OCA-proofness tidak cukup untuk menjamin pendapatan nol. Sekarang kami menunjukkan bahwa untuk mekanisme deterministik, menambahkan properti MMIC sudah cukup untuk mendapatkan hasil pendapatan 0 secara umum.

\ Teorema 4.1. Setiap mekanisme deterministik DSIC+MMIC+1-OCA-proof memiliki pendapatan penambang 0.

\

\ Namun, kami dapat memberikan karakterisasi yang bermakna bahkan ketika menghapus kondisi DSIC. Karakterisasi, yang diberikan dalam Lemma 4.3, tetap sangat mirip, meskipun dengan kebebasan lebih untuk menentukan aturan pembayaran.

\

\ Kami menyimpulkan bahwa pembakaran untuk semua nilai yang dialokasikan adalah beberapa konstanta R. Sekarang kami membandingkan R dengan r yang kami miliki untuk aturan alokasi.

\ Kami menyimpulkan bahwa R = r, yang menghasilkan karakterisasi yang ditentukan.

\ Ini memungkinkan kami untuk lebih mengkarakterisasi aturan alokasi dan pembakaran secara lebih umum, untuk mekanisme deterministik 1-OCA-proof.

\ Lemma 4.4. Setiap mekanisme deterministik 1-OCA-proof a, p, β persis dalam bentuk berikut: Untuk beberapa r ≥ 0, mekanisme mengalokasikan item kepada penawar tertinggi dengan syarat memiliki nilai lebih tinggi dari r, atau tidak mengalokasikan item sama sekali. Kapanpun dialokasikan, pembakaran adalah tepat r. Yaitu,

\

\

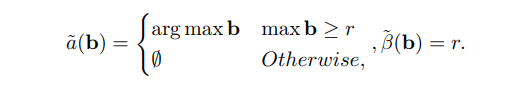
\ Sekarang kami dapat secara tepat mengkarakterisasi dua kelas mekanisme: Kelas mekanisme deterministik DSIC+1-OCA-proof, dan kelas mekanisme deterministik MMIC+1-OCA-proof.

\

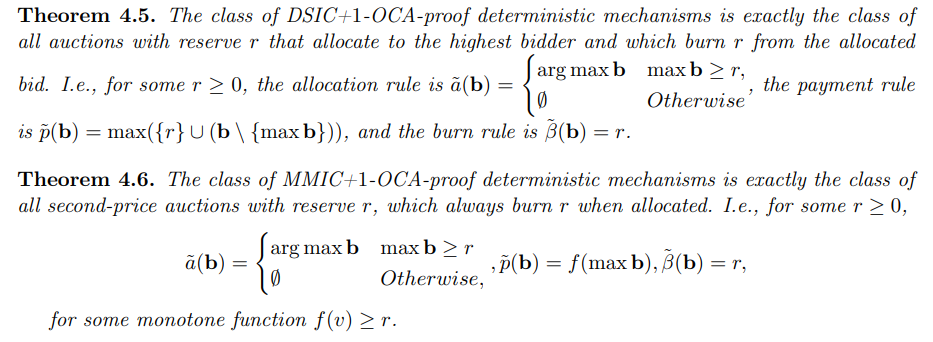
\ Karakterisasi yang tepat ini sekarang memungkinkan kami untuk menyimpulkan dengan hal berikut:

Teorema 4.7. Tidak pernah mengalokasikan item adalah satu-satunya mekanisme deterministik DSIC+MMIC+1-OCA-proof.

\ Bukti. Ini mengikuti dari Teorema 4.5 dan Teorema 4.6, karena dua kelas yang dikarakterisasi dalam hasil ini hanya memiliki mekanisme trivial yang sama (mengambil r = ∞). Untuk melihat ini secara intuitif, pertimbangkan kelas lelang harga kedua dengan cadangan r dan pembakaran konstan r dari Teorema 4.5. Lelang harga kedua tidak MMIC karena penambang dapat menambahkan penawar palsu yang secara sembarang dekat dengan tawaran pemenang untuk meningkatkan pembayaran.

\

5 Mekanisme Teracak OCA-proof

Sekarang kami memperluas diskusi ke mekanisme OCA-proof teracak. Untuk mekanisme teracak, kami mempertimbangkan pengertian OCA-proofness yang lebih kuat (daripada 1-OCA-proofness). Kami melakukannya untuk menghindari kekacauan dalam definisi, karena dalam mekanisme teracak koalisi pemenang mungkin sangat perlu mencakup semua penawar (karena masing-masing memiliki beberapa probabilitas fraksional untuk menang).

\ Sekarang kami mempertimbangkan properti alami untuk mekanisme:

\ Korolari 5.4. Berdasarkan Lemma 5.3, mekanisme DSIC+OCA-proof yang invarian skala tidak membakar biaya (yaitu, aturan pembakarannya adalah fungsi nol konstan), sementara dari Lemma 3.5 kita mendapatkan bahwa mekanisme DSIC+MMIC+OCAproof memiliki pembayaran sama dengan pembakaran dalam kasus penawar tunggal. Oleh karena itu, kita harus memiliki pembayaran 0 dalam kasus penawar tunggal, dan karenanya, dalam kasus penawar tunggal, item tersebut selalu atau tidak pernah dialokasikan.

\ Lemma 5.5. Untuk mekanisme DSIC+MMIC+OCA-proof, jika item selalu atau tidak pernah dialokasikan dalam kasus penawar tunggal, mekanisme tersebut harus trivial.

\

\ Dengan demikian, sebagai hasil langsung dari Korolari 5.4 dan Lemma 5.5, kita memiliki:

Korolari 5.6. Tidak ada mekanisme DSIC+MMIC+OCA-proof invarian skala yang non-trivial.

\ Argumen yang kami gunakan dalam Lemma 5.5 dapat diperluas untuk memungkinkan kami juga mengesampingkan kelas lelang yang memenuhi properti yang kami sebut probabilitas total alokasi konstan (CTPA), yang didefinisikan dalam Def. 5.7. Ini adalah kelas lelang yang menarik, karena mencakup semua lelang efisien (yang merupakan bagian dari kelas probabilitas total konstan 1 dari alokasi), termasuk lelang harga pertama dan harga kedua.

\

\

\

\ dan dengan demikian berdasarkan kelayakan Pers. (1):

\ Perhatikan bahwa ini adalah sisi kiri dari Lemma 5.12 di mana kita mempertimbangkan tawaran B · b, A · b. Kita dapat mengulangi cara kita mengembangkan Pers. (14) (untuk kasus tawaran A · b, A · b) dan, dengan mempertimbangkan bahwa penambang menghilangkan tawaran B · b, dapatkan:

\ Selanjutnya, untuk kasus dua penawar, kita dapat menunjukkan batas atas dan bawah yang berguna tentang seberapa banyak fungsi harus "mendukung" penawar yang lebih tinggi:

\

\

\

\

:::info Penulis:

(1) Yotam Gafni, Institut Weizmann ([email protected]);

(2) Aviv Yaish, Universitas Ibrani, Yerusalem ([email protected]).

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC BY 4.0 DEED.

:::

\