Memahami Kesalahan Aproksimasi dan Kompleksitas Kueri dalam Perutean WormHole

Tabel Tautan

Abstrak dan 1. Pendahuluan

1.1 Kontribusi Kami

1.2 Pengaturan

1.3 Algoritma

1. Karya Terkait

2. Algoritma

   3.1 Fase Dekomposisi Struktural

   3.2 Fase Perutean

   3.3 Varian WormHole

3. Analisis Teoretis

   4.1 Pendahuluan

   4.2 Sublinearitas Cincin Dalam

   4.3 Kesalahan Aproksimasi

   4.4 Kompleksitas Kueri

4. Hasil Eksperimental

   5.1 WormHole𝐸, WormHole𝐻 dan BiBFS

   5.2 Perbandingan dengan metode berbasis indeks

   5.3 WormHole sebagai primitif: WormHole𝑀

Referensi

4.3 Kesalahan Aproksimasi

Sekarang kita memiliki cincin dalam sublinear yang berisi inti Chung-Lu, kita harus menunjukkan bahwa perutean jalur melaluinya hanya menimbulkan penalti kecil. Secara intuitif, semakin besar cincin dalam, semakin mudah untuk memenuhi hal ini: jika cincin dalam adalah seluruh graf, pernyataan tersebut berlaku secara trivial. Oleh karena itu tantangannya terletak pada menunjukkan bahwa kita dapat mencapai jaminan yang kuat dalam hal akurasi bahkan dengan cincin dalam sublinear. Kami membuktikan bahwa WormHole menimbulkan kesalahan aditif paling banyak 𝑂(loglog𝑛) untuk semua pasangan, yang jauh lebih kecil daripada diameter Θ(log𝑛).

\

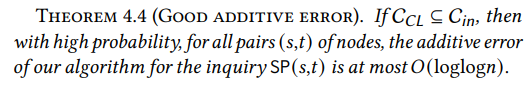
\ Hasil di atas berlaku dengan probabilitas tinggi bahkan dalam kasus terburuk. Yaitu, untuk semua pasangan (𝑠,𝑡) vertex dalam graf, panjang jalur yang dikembalikan oleh WormHole paling banyak 𝑂(loglog𝑛) lebih tinggi daripada jarak sebenarnya antara 𝑠 dan 𝑡. Ini secara trivial menyiratkan bahwa kesalahan aditif rata-rata WormHole, dengan probabilitas tinggi, dibatasi oleh jumlah yang sama.

\

\

4.4 Kompleksitas Kueri

Ingat model kueri node dalam makalah ini (lihat §1.2): dimulai dari satu node, kita diizinkan untuk secara iteratif membuat kueri, di mana setiap kueri mengambil daftar tetangga dari node 𝑣 pilihan kita. Kita tertarik pada kompleksitas kueri, yaitu jumlah kueri yang diperlukan untuk melakukan operasi tertentu.

\ \

\ \ Hasil pertama adalah batas atas pada kinerja kita.

\ \

\ \ Sketsa Bukti. Untuk pertanyaan SP(𝑢, 𝑣) yang diberikan, kami memberikan batas atas pada kompleksitas kueri BFS yang dimulai pada 𝑢, dan demikian pula untuk 𝑣; total kompleksitas kueri adalah jumlah dari kedua kuantitas ini.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info Penulis:

(1) Talya Eden, Universitas Bar-Ilan ([email protected]);

(2) Omri Ben-Eliezer, MIT ([email protected]);

(3) C. Seshadhri, UC Santa Cruz ([email protected]).

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC BY 4.0.

:::

\