Rumus yang Lebih Sederhana untuk Pendekatan Kurva Menggunakan Segmen Busur

Tabel Tautan

ABSTRAK

1 PENDAHULUAN

2 PERATAAN DAN PENDEKATAN BUSUR KURVA

3 SPIRAL EULER DAN KURVA PARALELNYA

4 KURVA PARALEL YANG DIRATAKAN

5 METRIK KESALAHAN UNTUK PENDEKATAN DENGAN BUSUR

6 EVOLUT

7 KONVERSI DARI BÉZIER KUBIK KE SPIRAL EULER

8 IMPLEMENTASI GPU

9 HASIL

KESIMPULAN, PEKERJAAN MASA DEPAN DAN REFERENSI

\

METRIK KESALAHAN UNTUK PENDEKATAN DENGAN BUSUR

Masalah pendekatan kurva dengan urutan segmen busur memiliki literatur yang luas, tetapi tidak ada solusi yang dipublikasikan yang cukup sesuai untuk aplikasi kami. Masalah khusus pendekatan spiral Euler dengan busur dipertimbangkan dalam Meek dan Walton [2004] menggunakan skema subdivisi adaptif "potong lalu ukur", tetapi solusi mereka memiliki kualitas buruk; berskala sebagai 𝑂(1/𝑛 2 ), sementara 𝑂(1/𝑛 3 ) dapat dicapai. Hasilnya ditingkatkan "sedikit" oleh Narayan [2014].

\ Literatur juga berisi hasil optimal, yaitu Maier [2014] dan Nuntawisuttiwong dan Dejdumrong [2021], tetapi dengan biaya yang cukup besar; kedua pendekatan mengklaim kompleksitas waktu 𝑂(𝑛 2 ). Benang merah untuk semua hasil ini adalah bahwa mereka memecahkan masalah yang lebih sulit: mengadopsi batasan bahwa urutan busur yang dihasilkan adalah kontinu 𝐺 1. Meskipun diinginkan untuk banyak aplikasi, batasan ini tidak diperlukan untuk merender garis luar stroke.

\ Bahkan dengan batasan ini dilonggarkan, diskontinuitas sudut dari pendekatan busur sangat kecil dibandingkan dengan perataan ke garis. Pendekatan kami didasarkan pada metrik kesalahan sederhana, mirip dengan yang digunakan untuk perataan ke segmen garis. Detail metrik (khususnya, penyesuaian konstanta) diperoleh secara empiris, meskipun kami menduga bahwa batas analitik yang lebih ketat dapat diperoleh. Dalam praktiknya, ini bekerja dengan sangat baik; cara terbaik untuk mengamati itu adalah alat pengujian interaktif, yang disediakan dalam materi tambahan.

Metrik kesalahan yang diusulkan adalah sebagai berikut. Perkiraan kesalahan jarak untuk kurva dengan panjang 𝑠ˆ adalah:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Untuk segmen spiral Euler, 𝜅 ′ (𝑠) konstan dan dengan demikian metrik kesalahan ini menjadi hampir sepele. Dengan 𝑛 subdivisi, perkiraan jarak adalah 𝑠 3𝜅 ′ 120𝑛 3 . Menyelesaikan untuk 𝑛, kita mendapatkan 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 subdivisi, dan itu dibagi secara merata berdasarkan panjang busur, karena kepadatan subdivisi konstan di seluruh kurva, sama seperti kasus perataan busur ke garis. Luar biasanya, pendekatan kurva paralel spiral Euler dengan segmen busur hampir sama sederhana dengan pendekatan spiral Euler ke busur.

\ Seperti dalam perataan ke garis, parameter untuk kurva adalah panjang busur dari spiral Euler asal. Kepadatan subdivisi kemudian konstan, dan hanya diperlukan sedikit penyesuaian pada rumus untuk menghitung jumlah subdivisi, dengan mempertimbangkan variasi kelengkungan tambahan dari offset oleh ℎ (setengah lebar garis). Rumus yang direvisi adalah:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Rumus ini ditentukan secara empiris dengan curve-fitting nilai kesalahan yang diukur dari pendekatan kurva paralel spiral Euler ke busur, tetapi juga terinspirasi dengan menerapkan rumus metrik kesalahan umum ke persamaan analitis untuk kurva paralel spiral Euler, dan menghilangkan suku-suku orde tinggi. Derivasi yang lebih ketat, idealnya dengan batas kesalahan yang tegas, tetap menjadi pekerjaan masa depan.

\ Salah satu konsekuensi dari rumus ini adalah, karena kesalahan dalam hal nilai absolut dari ℎ, terlepas dari tanda, pendekatan busur yang sama dapat digunakan untuk kedua sisi stroke. Lihat Gambar 8 untuk perbandingan antara perataan ke polyline dan pendekatan dengan segmen busur. Versi segmen busur memiliki jauh lebih sedikit segmen pada toleransi yang sama, sambil mempertahankan kualitas visual yang sangat tinggi.

EVOLUT

Dalam spesifikasi yang berprinsip dan benar untuk stroking [19], kurva paralel hanya cukup untuk segmen di mana kelengkungan

\

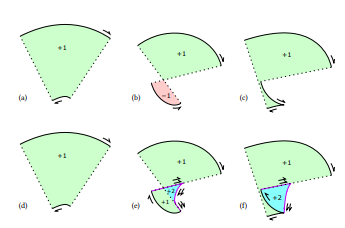
\ tidak melebihi setengah lebar resiprokal. Ketika itu terjadi, segmen tambahan harus digambar, termasuk evolut dari kurva asli. Secara umum, evolut dari Bézier kubik adalah kurva yang sangat kompleks, memerlukan teknik pendekatan. Sebaliknya, evolut dari spiral Euler (𝜅 = 𝑎𝑠) adalah spiral lain dengan persamaan Cesàro sederhana, yaitu 𝜅 = −𝑎 −1 𝑠 −3 , contoh dari hasil umum bahwa evolut dari kurva log-aesthetic adalah kurva log-aesthetic lainnya [26].

\ Perataan evolut ini juga mudah; kepadatan subdivisi sebanding dengan 𝑠 −0.5 di mana 𝑠 adalah parameter panjang busur dari spiral Euler yang mendasarinya (dan diterjemahkan sehingga 𝑠 = 0 adalah titik infleksi). Dengan demikian, integralnya adalah 2 √ 𝑠, dan integral inversnya hanyalah pengkuadratan. Dengan demikian, perataan evolut dari spiral Euler lebih sederhana daripada perataan kurva paralelnya. E

\ fek dari penambahan evolut untuk mencapai kebenaran yang kuat ditunjukkan pada Gambar 9. Segmen evolut tambahan dan garis penghubung dikeluarkan dua kali, untuk membuat nomor putaran konsisten dan menghasilkan garis luar yang kedap air. Semua nomor putaran positif, sehingga rendering dengan aturan putaran bukan nol menghasilkan render akhir yang benar.

:::info Penulis:

1. Raph Levien
2. Arman Uguray

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC 4.0.

:::

\