Bagaimana Algoritma Serakah Membentuk Imbalan Penambang dalam Jaringan Blockchain

Tabel Tautan

Abstrak dan 1. Pendahuluan

1.1 Pendekatan Kami

1.2 Hasil & Peta Jalan Kami

1.3 Karya Terkait

1. Model dan Pemanasan dan 2.1 Model Blockchain

   2.2 Penambang

   2.3 Model Permainan

   2.4 Pemanasan: Fungsi Alokasi Serakah

2. Kasus Deterministik dan 3.1 Batas Atas Deterministik

   3.2 Kelas Fungsi Alokasi Bias-Kesegeraan

3. Kasus Teracak

4. Diskusi dan Referensi

• A. Bukti yang Hilang untuk Bagian 2, 3
• B. Bukti yang Hilang untuk Bagian 4
• C. Glosarium

\

2.3 Model Permainan

Kami meneliti permainan antara lawan dan penambang. Perspektif ini bertujuan untuk mengukur berapa banyak pendapatan yang mungkin hilang oleh penambang karena pengetahuan yang tidak lengkap tentang transaksi masa depan saat mengalokasikan transaksi yang saat ini diketahui ke blok yang akan datang. Dalam hal ini, pengguna aktif dalam sistem dapat dianggap sebagai "alam" yang maha tahu dan berlawanan, yang menciptakan jadwal transaksi terburuk. Fungsi alokasi tidak memiliki pengetahuan tentang transaksi masa depan yang akan dikirim oleh lawan, sehingga perencanaan optimal berdasarkan informasi parsial yang diungkapkan oleh transaksi sebelumnya mungkin bukan tindakan terbaik. Namun, agak mengejutkan, kami kemudian menunjukkan bahwa itu memang demikian. Mengingat tingkat diskon penambang, ada ketegangan konseptual antara memasukkan transaksi dengan biaya terbesar dan yang memiliki TTL terendah. Dengan demikian, kualitas fungsi alokasi x dikuantifikasi dengan membandingkannya dengan fungsi terbaik yang mungkin x′, ketika menghadapi ψ yang berlawanan dalam kasus terburuk. Kuantitas yang dihasilkan disebut rasio kompetitif x. Untuk tetap kompatibel dengan literatur tentang penjadwalan paket, kami mendefinisikan rasio kompetitif sebagai kinerja offline terbaik yang mungkin dibagi dengan kinerja online fungsi alokasi, bukan sebaliknya, dan karenanya kami memiliki Rx ≥ 1. Batas atas kemudian dicapai dengan menemukan fungsi alokasi yang menjamin kinerja yang baik, dan batas bawah dicapai dengan menunjukkan bahwa tidak ada fungsi alokasi yang dapat menjamin kinerja yang lebih baik.

\ \

\ \ \

2.4 Pemanasan: Fungsi Alokasi Serakah

Fungsi alokasi Serakah, didefinisikan dalam Definisi 2.6, mungkin merupakan algoritma klasik untuk masalah penjadwalan paket, dan telah dieksplorasi oleh literatur sebelumnya untuk kasus tanpa diskon. Selain itu, bukti empiris menunjukkan bahwa sebagian besar penambang dengan serakah mengalokasikan transaksi ke blok. Karya sebelumnya menunjukkan bahwa di Bitcoin dan Ethereum, transaksi yang membayar biaya lebih tinggi umumnya memiliki waktu tunggu mempool yang lebih rendah, yang berarti bahwa mereka dimasukkan relatif cepat dalam blok [MACG20; PORH22; TFWM21; LLNZZZ22]. Memang, algoritma pemilihan transaksi default untuk Bitcoin Core (implementasi referensi untuk klien Bitcoin) dan geth (klien eksekusi Ethereum yang paling populer), memprioritaskan transaksi berdasarkan biayanya, meskipun perilaku default keduanya dapat diganti. Oleh karena itu, menarik untuk melihat kinerja pendekatan ini.

\ Definisi 2.6 (Fungsi alokasi Serakah). Diberikan beberapa set transaksi S, fungsi alokasi Serakah memilih transaksi dengan pembayaran tertinggi yang ada dalam set S, mengabaikan TTL:

\

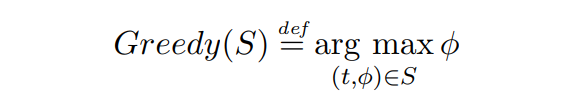
\ Jika ada beberapa transaksi dengan biaya yang sama, yang memiliki TTL terendah lebih diutamakan.

\ Dalam Contoh 2.7, kami mengilustrasikan bagaimana kinerja Serakah mungkin bergantung pada tingkat diskon.

\ Contoh 2.7. Kami memeriksa kinerja Serakah dengan lawan ψ berikut.

\

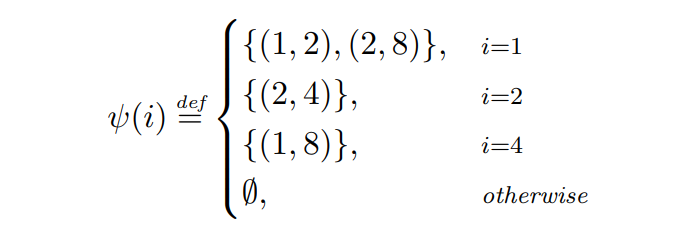
\ Jadwal transaksi yang didefinisikan oleh ψ digambarkan dalam Gambar 1. Pada giliran 1, lawan menyiarkan dua transaksi: (1, 2) yang kedaluwarsa pada akhir giliran dan memiliki biaya 2, dan (2, 4) yang membayar biaya sebesar 4 dan kedaluwarsa pada akhir giliran berikutnya. Karena Serakah memprioritaskan transaksi dengan biaya lebih tinggi, ia akan mengalokasikan (2, 4), sambil membiarkan transaksi lain kedaluwarsa. Pada giliran berikutnya, lawan menyiarkan satu transaksi dengan TTL 2 dan biaya 6, yang merupakan satu-satunya yang tersedia untuk Serakah pada giliran itu, dan dengan demikian akan dialokasikan. Pada langkah 3, lawan tidak mengeluarkan transaksi apa pun, dan pada langkah 4, transaksi (1, 8) disiarkan dan kemudian dialokasikan oleh Serakah.

\

\

\ Dalam Lemma 2.8, kami membatasi rasio kompetitif Serakah, sebagai fungsi dari tingkat diskon.

\

\

\

\

:::info Penulis:

(1) Yotam Gafni, Institut Weizmann ([email protected]);

(2) Aviv Yaish, Universitas Ibrani, Yerusalem ([email protected]).

:::

:::info Makalah ini tersedia di arxiv di bawah lisensi CC BY 4.0 DEED.

:::

\